线性代数对于深度学习和科学计算至关重要,它一直是 PyTorch 的核心部分。PyTorch 1.9 通过 torch.linalg 模块扩展了 PyTorch 对线性代数运算的支持。该模块在此处有文档说明,包含 26 个运算符,包括比旧版 PyTorch 运算符更快、更易用的版本,NumPy 线性代数模块中的每个函数都扩展了加速器和自动微分支持,以及一些全新的运算符。这使得 torch.linalg 对 NumPy 用户来说非常熟悉,并且是 PyTorch 线性代数支持的激动人心的更新。
PyTorch 中的 NumPy 风格线性代数
如果您熟悉 NumPy 的线性代数模块,那么使用 torch.linalg 将会很容易。在大多数情况下,它是一个即插即用的替代品。让我们以使用 Cholesky 分解从多元正态分布中抽取样本为例,来说明这一点:
import numpy as np
# Creates inputs
np.random.seed(0)
mu_np = np.random.rand(4)
L = np.random.rand(4, 4)
# Covariance matrix sigma is positive-definite
sigma_np = L @ L.T + np.eye(4)
normal_noise_np = np.random.standard_normal(mu_np.size)
def multivariate_normal_sample_np(mu, sigma, normal_noise):
return mu + np.linalg.cholesky(sigma) @ normal_noise
print("Random sample: ",
multivariate_normal_sample_np(mu_np, sigma_np, normal_noise_np))
: Random sample: [2.9502426 1.78518077 1.83168697 0.90798228]
现在让我们看看同样的采样器在 PyTorch 中的实现:
import torch
def multivariate_normal_sample_torch(mu, sigma, normal_noise):
return mu + torch.linalg.cholesky(sigma) @ normal_noise
这两个函数是相同的,我们可以通过用相同的参数调用函数并将参数包装成 PyTorch 张量来验证它们的行为:
# NumPy arrays are wrapped as tensors and share their memory
mu_torch = torch.from_numpy(mu_np)
sigma_torch = torch.from_numpy(sigma_np)
normal_noise_torch = torch.from_numpy(normal_noise_np)
multivariate_normal_sample_torch(mu_torch, sigma_torch, normal_noise_torch)
: tensor([2.9502, 1.7852, 1.8317, 0.9080], dtype=torch.float64)
唯一的区别在于 PyTorch 默认如何打印张量。
Cholesky 分解还可以帮助我们快速计算非退化多元正态分布的概率密度函数。在该计算中,昂贵的项之一是协方差矩阵行列式的平方根。利用行列式的性质和 Cholesky 分解,我们可以比原始计算更快地计算出相同的结果。下面是一个 NumPy 程序,展示了这一点:
sqrt_sigma_det_np = np.sqrt(np.linalg.det(sigma_np))
sqrt_L_det_np = np.prod(np.diag(np.linalg.cholesky(sigma_np)))
print("|sigma|^0.5 = ", sqrt_sigma_det_np)
: |sigma|^0.5 = 4.237127491242027
print("|L| = ", sqrt_L_det_np)
: |L| = 4.237127491242028
这里是相同的验证在 PyTorch 中:
sqrt_sigma_det_torch = torch.sqrt(torch.linalg.det(sigma_torch))
sqrt_L_det_torch = torch.prod(torch.diag(torch.linalg.cholesky(sigma_torch)))
print("|sigma|^0.5 = ", sqrt_sigma_det_torch)
: |sigma|^0.5 = tensor(4.2371, dtype=torch.float64)
print("|L| = ", sqrt_L_det_torch)
: |L| = tensor(4.2371, dtype=torch.float64)
我们可以使用 PyTorch 的内置基准工具来衡量运行时间的差异:
import torch.utils.benchmark as benchmark
t0 = benchmark.Timer(
stmt='torch.sqrt(torch.linalg.det(sigma))',
globals={'sigma': sigma_torch})
t1 = benchmark.Timer(
stmt='torch.prod(torch.diag(torch.linalg.cholesky(sigma)))',
globals={'sigma': sigma_torch})
print(t0.timeit(100))
: torch.sqrt(torch.linalg.det(sigma))
80.80 us
1 measurement, 100 runs , 1 thread
print(t1.timeit(100))
: torch.prod(torch.diag(torch.linalg.cholesky(sigma)))
11.56 us
1 measurement, 100 runs , 1 thread
证明使用 Cholesky 分解的方法可以显著更快。在幕后,PyTorch 的线性代数模块使用 OpenBLAS 或 MKL 实现的 LAPACK 标准来最大化其 CPU 性能。
自动微分支持
PyTorch 的线性代数模块不仅实现了与 NumPy 线性代数模块相同的函数(以及一些额外的函数),而且还通过 autograd 和 CUDA 支持扩展了它们。
让我们看看一个非常简单的程序,它只计算一个逆矩阵及其梯度的运算,以展示 autograd 是如何工作的:
t = torch.tensor(((1, 2), (3, 4)), dtype=torch.float32, requires_grad=True)
inv = torch.linalg.inv(t)
inv.backward(torch.ones_like(inv))
print(t.grad)
: tensor([[-0.5000, 0.5000],
[ 0.5000, -0.5000]])
我们可以通过自己定义 autograd 公式来在 NumPy 中模拟相同的计算:
a = np.array(((1, 2), (3, 4)), dtype=np.float32)
inv_np = np.linalg.inv(a)
def inv_backward(result, grad):
return -(result.transpose(-2, -1) @ (grad @ result.transpose(-2, -1)))
grad_np = inv_backward(inv_np, np.ones_like(inv_np))
print(grad_np)
: [[-0.5 0.5]
[ 0.5 -0.5]]
当然,随着程序变得越来越复杂,拥有内置的 autograd 支持就变得方便了,PyTorch 的线性代数模块支持实数和复数的 autograd。
CUDA 支持
对 autograd 和加速器(如 CUDA 设备)的支持是 PyTorch 的核心部分。 torch.linalg 模块是在 NVIDIA 的 PyTorch 和 cuSOLVER 团队的帮助下开发的,他们利用 cuSOLVER、cuBLAS 和 MAGMA 库优化了其在 CUDA 设备上的性能。这些改进使得 PyTorch 的 CUDA 线性代数操作比以往任何时候都要快。例如,让我们看看 PyTorch 1.9 的 torch.linalg.cholesky 与已弃用的 PyTorch 1.8 的 torch.cholesky 的性能对比:
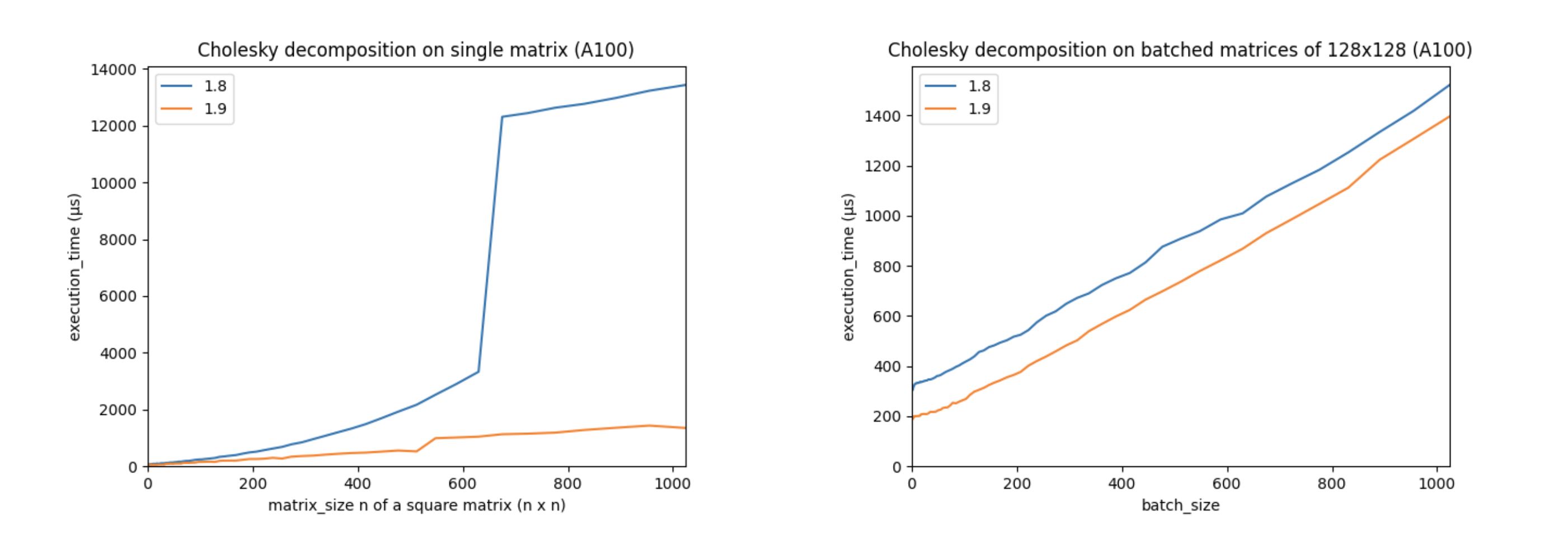
(以上图表是在使用 A100 GPU、CUDA 11.3、cuSOLVER 11.1.1.58 和 MAGMA 2.5.2 的情况下创建的。矩阵使用双精度。)
这些图表显示,在更大的矩阵上性能显著提高,并且批处理性能全面提升。其他线性代数操作,包括 torch.linalg.qr 和 torch.linalg.lstsq ,其 CUDA 性能也得到了提升。
超越 NumPy
除了提供 NumPy 线性代数模块的所有功能,并支持自动微分和加速器外, torch.linalg 还增加了一些自己的新功能。NumPy 的 linalg.norm 不允许用户在任意子维度集上计算向量范数,因此为了实现这一功能,我们增加了 torch.linalg.vector_norm 。我们还开始对 PyTorch 中的其他线性代数功能进行现代化改造,因此我们创建了 torch.linalg.householder_product 来替换旧的 torch.orgqr ,并且我们计划在未来继续添加更多的线性代数功能。
PyTorch 中线性代数的未来
torch.linalg 模块运行速度快,与自动微分和加速器兼容性良好。它已经在 botorch 等库中使用。但我们不会止步于此。我们计划继续更新 PyTorch 现有的更多线性代数功能(如 torch.lobpcg ),并提供对低秩和稀疏线性代数的更多支持。我们还希望听到您对我们如何改进的反馈,所以开始在论坛上发起讨论或在我们的 GitHub 上提交问题并分享您的想法。
我们期待听到您的反馈,并看看社区如何使用 PyTorch 的新线性代数功能!