确保您的输入采用正确的内存格式可以显著影响您的 PyTorch 视觉模型的运行时间。如有疑问,请选择 Channels Last 内存格式。
当处理 PyTorch 中的视觉模型,这些模型接受多媒体(例如图像 Tensorts)作为输入时,Tensor 的内存格式可以显著影响模型在移动平台上使用 CPU 后端和 XNNPACK 时的推理执行速度。这在服务器平台上的训练和推理也同样适用,但对于移动设备和用户来说,延迟尤其关键。
本文大纲
- 深入探讨 C++中矩阵存储/内存表示,介绍行主序和列主序。
- 在相同或不同的存储表示顺序中循环矩阵的影响,以及一个示例。
- Cachegrind 简介;一个用于检查代码缓存友好性的工具。
- PyTorch 算子支持的内存格式。
- 使用 XNNPACK 优化确保高效模型执行的最佳实践示例
C++中的矩阵存储表示
图像被作为多维张量输入到 PyTorch 机器学习模型中。这些张量具有特定的内存格式。为了更好地理解这一概念,让我们看看二维矩阵在内存中的存储方式。
从广义上讲,有两种主要方式在内存中高效存储多维数据。
- 行主序:在这种格式中,矩阵按行顺序存储,每行存储在内存中,在下一行之前。即第 N 行在 N+1 行之前。
- 列主序:在这种格式中,矩阵按列顺序存储,每列存储在内存中,在下一列之前。即第 N 列在 N+1 列之前。
下面可以直观地看到差异。
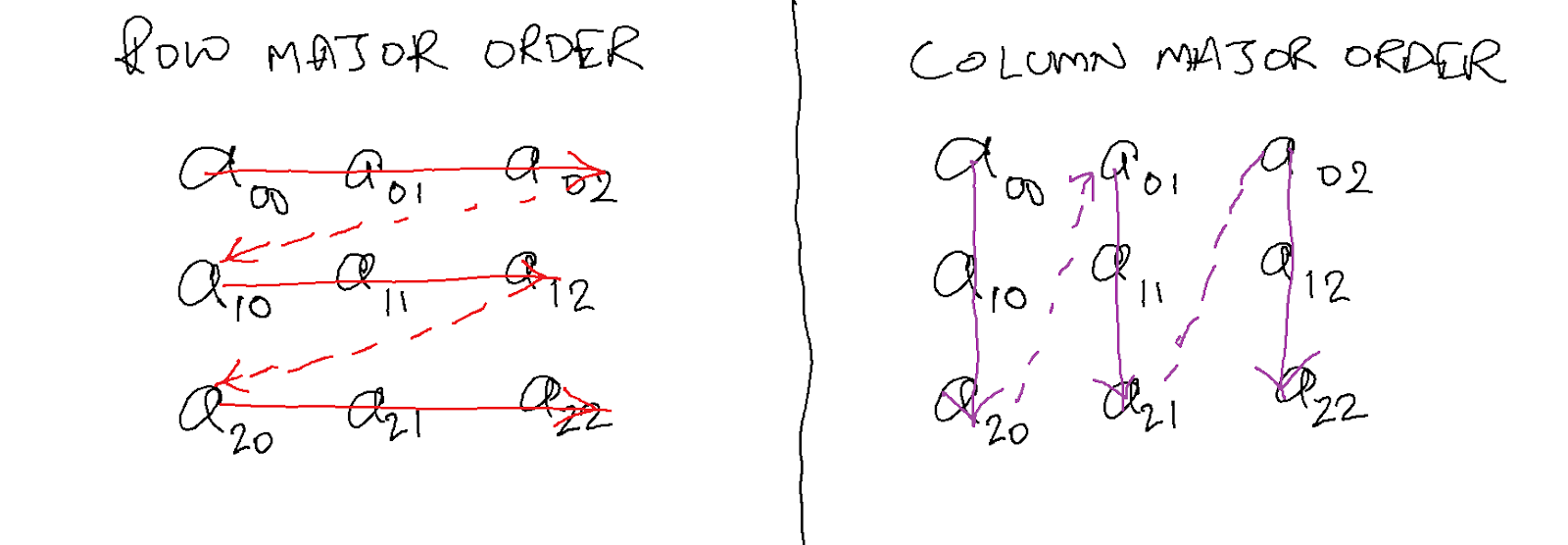
C++以行主序格式存储多维数据。
高效访问二维数组的元素
与存储格式相似,访问二维数组数据有 2 种方式。
- 首先遍历行:处理完当前行的所有元素后,再处理下一行的任何元素。
- 首先遍历列:处理完当前列的所有元素后,再处理下一列的任何元素。
为了达到最大效率,应该始终以数据存储的格式访问数据。也就是说,如果数据以行主序存储,那么应该尝试按该顺序访问。
下面的代码(main.cpp)展示了访问 2D 4000x4000 矩阵所有元素的两种方法。
#include <iostream>
#include <chrono>
// loop1 accesses data in matrix 'a' in row major order,
// since i is the outer loop variable, and j is the
// inner loop variable.
int loop1(int a[4000][4000]) {
int s = 0;
for (int i = 0; i < 4000; ++i) {
for (int j = 0; j < 4000; ++j) {
s += a[i][j];
}
}
return s;
}
// loop2 accesses data in matrix 'a' in column major order
// since j is the outer loop variable, and i is the
// inner loop variable.
int loop2(int a[4000][4000]) {
int s = 0;
for (int j = 0; j < 4000; ++j) {
for (int i = 0; i < 4000; ++i) {
s += a[i][j];
}
}
return s;
}
int main() {
static int a[4000][4000] = {0};
for (int i = 0; i < 100; ++i) {
int x = rand() % 4000;
int y = rand() % 4000;
a[x][y] = rand() % 1000;
}
auto start = std::chrono::high_resolution_clock::now();
auto end = start;
int s = 0;
#if defined RUN_LOOP1
start = std::chrono::high_resolution_clock::now();
s = 0;
for (int i = 0; i < 10; ++i) {
s += loop1(a);
s = s % 100;
}
end = std::chrono::high_resolution_clock::now();
std::cout << "s = " << s << std::endl;
std::cout << "Time for loop1: "
<< std::chrono::duration<double, std::milli>(end - start).count()
<< "ms" << std::endl;
#endif
#if defined RUN_LOOP2
start = std::chrono::high_resolution_clock::now();
s = 0;
for (int i = 0; i < 10; ++i) {
s += loop2(a);
s = s % 100;
}
end = std::chrono::high_resolution_clock::now();
std::cout << "s = " << s << std::endl;
std::cout << "Time for loop2: "
<< std::chrono::duration<double, std::milli>(end - start).count()
<< "ms" << std::endl;
#endif
}
Let’s build and run this program and see what it prints.
g++ -O2 main.cpp -DRUN_LOOP1 -DRUN_LOOP2
./a.out
Prints the following:
s = 70
Time for loop1: 77.0687ms
s = 70
Time for loop2: 1219.49ms
loop1() 比 loop2() 快 15 倍。为什么?下面我们来找出原因!
使用 Cachegrind 测量缓存未命中
Cachegrind 是一个缓存分析工具,用于查看您的程序造成了多少 I1(一级指令)、D1(一级数据)和 LL(最后一级)缓存未命中。
让我们只用 loop1() 和 loop2() 构建我们的程序,看看这些函数的缓存友好性如何。
构建/运行/分析 just loop1()
g++ -O2 main.cpp -DRUN_LOOP1
valgrind --tool=cachegrind ./a.out
打印:
==3299700==
==3299700== I refs: 643,156,721
==3299700== I1 misses: 2,077
==3299700== LLi misses: 2,021
==3299700== I1 miss rate: 0.00%
==3299700== LLi miss rate: 0.00%
==3299700==
==3299700== D refs: 160,952,192 (160,695,444 rd + 256,748 wr)
==3299700== D1 misses: 10,021,300 ( 10,018,723 rd + 2,577 wr)
==3299700== LLd misses: 10,010,916 ( 10,009,147 rd + 1,769 wr)
==3299700== D1 miss rate: 6.2% ( 6.2% + 1.0% )
==3299700== LLd miss rate: 6.2% ( 6.2% + 0.7% )
==3299700==
==3299700== LL refs: 10,023,377 ( 10,020,800 rd + 2,577 wr)
==3299700== LL misses: 10,012,937 ( 10,011,168 rd + 1,769 wr)
==3299700== LL miss rate: 1.2% ( 1.2% + 0.7% )
编译并运行/配置 just loop2()
g++ -O2 main.cpp -DRUN_LOOP2
valgrind --tool=cachegrind ./a.out
打印:
==3300389==
==3300389== I refs: 643,156,726
==3300389== I1 misses: 2,075
==3300389== LLi misses: 2,018
==3300389== I1 miss rate: 0.00%
==3300389== LLi miss rate: 0.00%
==3300389==
==3300389== D refs: 160,952,196 (160,695,447 rd + 256,749 wr)
==3300389== D1 misses: 160,021,290 (160,018,713 rd + 2,577 wr)
==3300389== LLd misses: 10,014,907 ( 10,013,138 rd + 1,769 wr)
==3300389== D1 miss rate: 99.4% ( 99.6% + 1.0% )
==3300389== LLd miss rate: 6.2% ( 6.2% + 0.7% )
==3300389==
==3300389== LL refs: 160,023,365 (160,020,788 rd + 2,577 wr)
==3300389== LL misses: 10,016,925 ( 10,015,156 rd + 1,769 wr)
==3300389== LL miss rate: 1.2% ( 1.2% + 0.7% )
两次运行的主要区别是:
- D1 缺失:10M 对比 160M
- D1 误报率:6.2% vs 99.4%
如您所见, loop2() 比 loop1()导致许多许多更多的(约 16 倍)L1 数据缓存未命中。这就是为什么 loop1() 比 loop2()快约 15 倍的原因。
PyTorch 算子支持的内存格式
虽然 PyTorch 算子期望所有张量都使用通道优先(NCHW)维度格式,但 PyTorch 算子支持 3 种输出内存格式。
- 连续:张量内存的顺序与张量的维度相同。
- 通道最后:不考虑维度顺序,2 维(图像)张量在内存中以 HWC 或 NHWC(N:批次,H:高度,W:宽度,C:通道)张量的形式排列。维度可以以任何顺序排列。
- 通道最后 3d:对于 3 维张量(视频张量),内存以 THWC(时间,高度,宽度,通道)或 NTHWC(N:批次,T:时间,H:高度,W:宽度,C:通道)格式排列。维度可以以任何顺序排列。
通道最后格式被视觉模型优先考虑的原因是,PyTorch 使用的 XNNPACK(内核加速库)期望所有输入都采用通道最后格式,因此如果模型的输入不是通道最后格式,则必须首先将其转换为通道最后格式,这会额外增加一个操作。
此外,大多数 PyTorch 算子都保留了输入张量的内存格式,因此如果输入是通道优先,那么算子需要首先将其转换为通道最后,然后执行操作,然后再转换回通道优先。
当您结合加速算子更适合使用通道最后内存格式这一事实时,您会发现让算子返回通道最后内存格式对后续算子调用更有利,否则您将不得不让每个算子都转换为通道最后(这可能对特定算子更有效率)。
来自 XNNPACK 主页:
“XNNPACK 中的所有算子都支持 NHWC 布局,但还允许在通道维度上自定义步长”。
PyTorch 最佳实践
要从您的 PyTorch 视觉模型中获得最佳性能,请确保在将其输入模型之前,您的输入张量处于 Channels Last 内存格式。
通过优化模型以使用 XNNPACK 后端(只需在您的 torchscripted 模型上调用 optimize_for_mobile() 即可)可以获得更多的加速。请注意,如果输入是连续的,XNNPACK 模型将运行得更慢,所以请务必确保它处于 Channels-Last 格式。
展示加速效果的示例
在 Google Colab 上运行此示例 - 注意,Colab CPU 的运行时间可能无法反映准确性能;建议在您的本地机器上运行此代码。
import torch
from torch.utils.mobile_optimizer import optimize_for_mobile
import torch.backends.xnnpack
import time
print("XNNPACK is enabled: ", torch.backends.xnnpack.enabled, "\n")
N, C, H, W = 1, 3, 200, 200
x = torch.rand(N, C, H, W)
print("Contiguous shape: ", x.shape)
print("Contiguous stride: ", x.stride())
print()
xcl = x.to(memory_format=torch.channels_last)
print("Channels-Last shape: ", xcl.shape)
print("Channels-Last stride: ", xcl.stride())
## Outputs:
# XNNPACK is enabled: True
# Contiguous shape: torch.Size([1, 3, 200, 200])
# Contiguous stride: (120000, 40000, 200, 1)
# Channels-Last shape: torch.Size([1, 3, 200, 200])
# Channels-Last stride: (120000, 1, 600, 3)
对于连续和通道最后格式,输入形状保持不变。然而,如您在步幅中看到的那样,内部张量的布局已更改。现在,跨通道所需的跳跃次数仅为 1(而不是连续张量中的 40000)。这种更好的数据局部性意味着卷积层可以更快地访问给定像素的所有通道。现在,让我们看看内存格式如何影响运行时间:
from torchvision.models import resnet34, resnet50, resnet101
m = resnet34(pretrained=False)
# m = resnet50(pretrained=False)
# m = resnet101(pretrained=False)
def get_optimized_model(mm):
mm = mm.eval()
scripted = torch.jit.script(mm)
optimized = optimize_for_mobile(scripted) # explicitly call the xnnpack rewrite
return scripted, optimized
def compare_contiguous_CL(mm):
# inference on contiguous
start = time.perf_counter()
for i in range(20):
mm(x)
end = time.perf_counter()
print("Contiguous: ", end-start)
# inference on channels-last
start = time.perf_counter()
for i in range(20):
mm(xcl)
end = time.perf_counter()
print("Channels-Last: ", end-start)
with torch.inference_mode():
scripted, optimized = get_optimized_model(m)
print("Runtimes for torchscripted model: ")
compare_contiguous_CL(scripted.eval())
print()
print("Runtimes for mobile-optimized model: ")
compare_contiguous_CL(optimized.eval())
## Outputs (on an Intel Core i9 CPU):
# Runtimes for torchscripted model:
# Contiguous: 1.6711160129999598
# Channels-Last: 1.6678222839999535
# Runtimes for mobile-optimized model:
# Contiguous: 0.5712863490000473
# Channels-Last: 0.46113000699995155
结论
输入张量的内存布局可以显著影响模型的运行时间。对于视觉模型,建议使用通道最后内存格式以充分利用您的 PyTorch 模型。