在本文中,我们介绍了最近提出的随机权重平均(SWA)技术[1, 2],以及其在 torchcontrib 中的新实现。SWA 是一种简单的方法,可以在不增加额外成本的情况下提高深度学习在随机梯度下降(SGD)上的泛化能力,并且可以作为 PyTorch 中任何其他优化器的直接替换。SWA 具有广泛的应用和特性:
- SWA 已被证明可以显著提高计算机视觉任务中的泛化能力,包括在 ImageNet 和 CIFAR 基准测试上的 VGG、ResNets、Wide ResNets 和 DenseNets[1, 2]。
- SWA 在半监督学习和领域自适应的关键基准测试中提供了最先进的性能[2]。
- SWA 被证明可以改善深度强化学习中策略梯度方法的训练稳定性以及最终平均奖励[3]。
- SWA 的扩展可以获取高效的贝叶斯模型平均,以及深度学习中的高质量不确定性估计和校准[4]。
- SWA 用于低精度训练,SWALP,即使将所有数字量化到 8 位,包括梯度累加器,也能匹配全精度 SGD 的性能[5]。
简而言之,SWA 使用修改后的学习率计划对 SGD 遍历的权重进行等平均(见图 1 左面板)。SWA 解最终位于损失广泛平坦区域的中心,而 SGD 往往收敛到低损失区域的边界,这使得它容易受到训练和测试误差表面之间偏移的影响(见图 1 中间和右面板)。
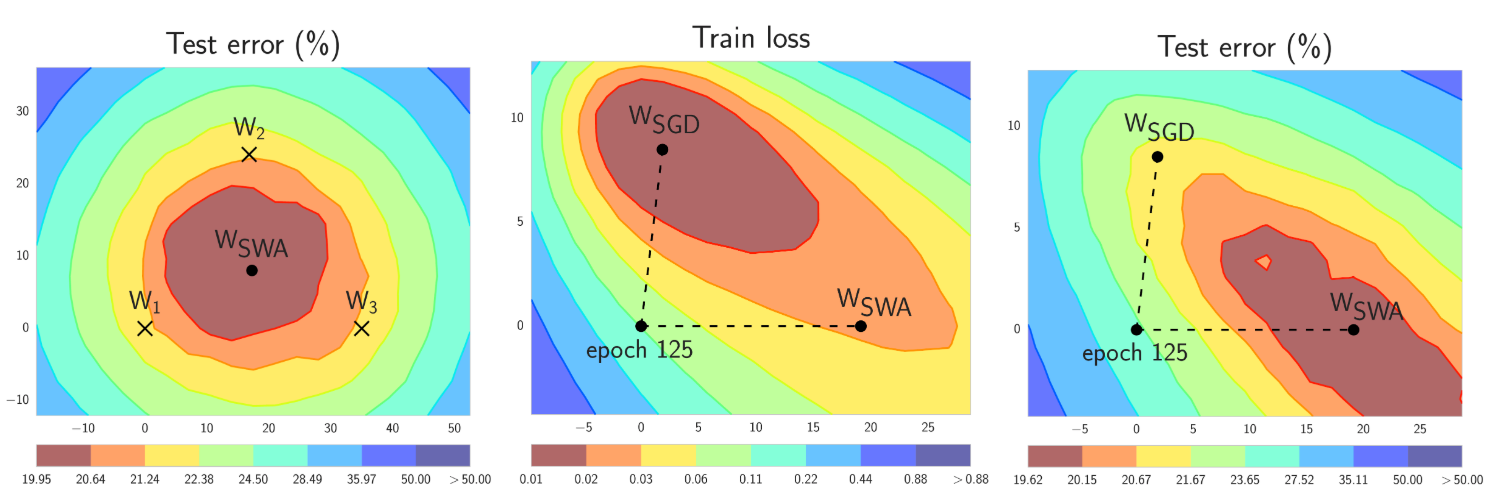
图 1. SWA 和 SGD 在 CIFAR-100 上的 Preactivation ResNet-164 的示意图[1]。左:三个 FGE 样本的测试误差表面和相应的 SWA 解(在权重空间中平均)。中间和右:测试误差和训练损失表面,显示了 SGD(在收敛时)和 SWA 的权重,它们从 SGD 相同的初始化开始,经过 125 个训练周期。请参阅[1]了解这些图是如何构建的。
使用 torchcontrib 中的新实现,使用 SWA(Stochastic Weight Averaging)与使用 PyTorch 中的任何其他优化器一样简单:
from torchcontrib.optim import SWA
...
...
# training loop
base_opt = torch.optim.SGD(model.parameters(), lr=0.1)
opt = torchcontrib.optim.SWA(base_opt, swa_start=10, swa_freq=5, swa_lr=0.05)
for _ in range(100):
opt.zero_grad()
loss_fn(model(input), target).backward()
opt.step()
opt.swap_swa_sgd()
您可以使用 SWA 类将 torch.optim 中的任何优化器包装起来,然后像往常一样训练您的模型。当训练完成后,您只需调用 swap_swa_sgd() 来将您的模型权重设置为它们的 SWA 平均值。以下我们将详细解释 SWA 过程和 SWA 类的参数。我们强调,SWA 可以与任何优化过程结合使用,例如与 Adam 结合,就像它可以与 SGD 结合一样。
这只是平均 SGD 吗?
从高层次来看,平均 SGD 迭代可以追溯到几十年的凸优化[6, 7],有时也被称为 Polyak-Ruppert 平均或平均 SGD。但细节很重要。平均 SGD 通常与递减的学习率和指数移动平均结合使用,通常用于凸优化。在凸优化中,重点是提高收敛速度。在深度学习中,这种形式的平均 SGD 平滑了 SGD 迭代的轨迹,但与 SGD 本身并没有太大的不同。
与之相反,SWA 关注于使用修改后的循环或高恒定学习率的 SGD 迭代的平均,并利用特定于深度学习的训练目标平坦性来提高泛化能力[8]。
随机权重平均
SWA 能够工作的两个重要因素。首先,SWA 使用修改后的学习率计划,使得 SGD 继续探索高性能网络集合,而不是简单地收敛到一个单一解。例如,我们可以使用标准的衰减学习率策略进行前 75%的训练时间,然后为剩余的 25%时间设置一个合理的高恒定值(见图 2)。第二个因素是对 SGD 遍历的网络权重进行平均。例如,我们可以在训练时间的最后 25%内,对每个 epoch 结束时获得的权重进行运行平均(见图 2)。
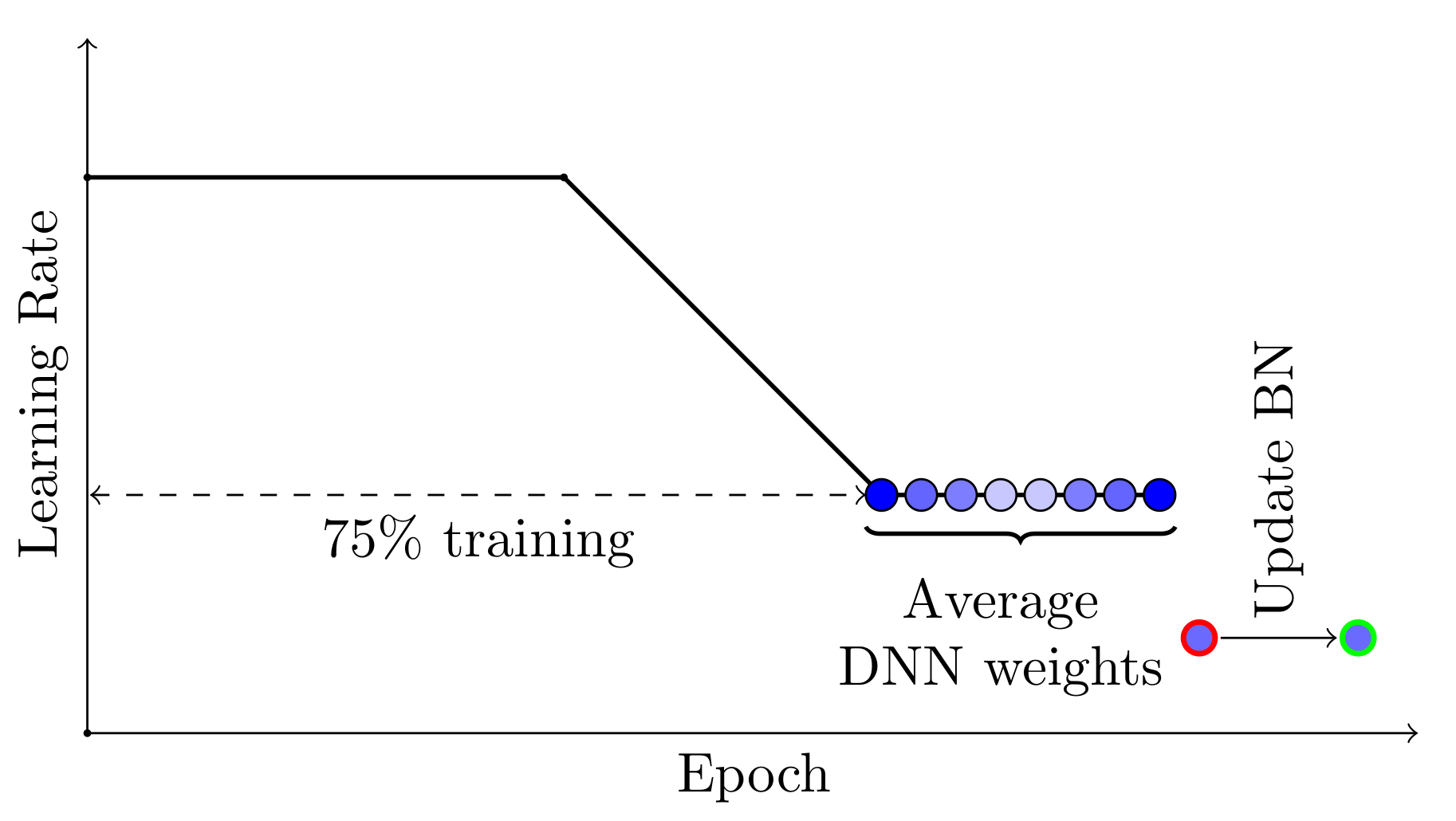
图 2. SWA 采用的学习率计划的示意图。前 75%的训练使用标准衰减计划,然后剩余 25%使用高常数值。SWA 平均值在训练的最后 25%时间内形成。
在我们的实现中, SWA 优化器的自动模式允许我们运行上述描述的流程。要在自动模式下运行 SWA,只需将您选择的优化器 base_opt (可以是 SGD、Adam 或任何其他 torch.optim.Optimizer )用 SWA(base_opt, swa_start, swa_freq, swa_lr) 包装。经过 swa_start 优化步骤后,学习率将切换到恒定值 swa_lr ,并在每个 swa_freq 优化步骤结束时,将权重的快照添加到 SWA 的运行平均值中。一旦运行 opt.swap_swa_sgd() ,您的模型权重将被替换为它们的 SWA 运行平均值。
批标准化
一个需要注意的重要细节是批量归一化。批量归一化层在训练过程中计算激活的运行统计。请注意,SWA 权重的平均值在训练过程中永远不会用于预测,因此批量归一化层在您使用 opt.swap_swa_sgd() 重置模型权重后不会计算激活统计。要计算激活统计,您只需使用 SWA 模型在训练完成后对您的训练数据进行一次前向传递。在 SWA 类中,我们提供了一个辅助函数 opt.bn_update(train_loader, model) 。它通过在 train_loader 数据加载器上执行前向传递来更新模型中每个批量归一化层的激活统计。您只需要在训练结束时调用此函数一次。
高级学习率调度
SWA 可以与任何鼓励探索解的平坦区域的调度一起使用。例如,您可以在训练时间的最后 25%使用周期性学习率,而不是恒定值,并平均每个周期内对应于最低学习率值的网络权重(见图 3)。
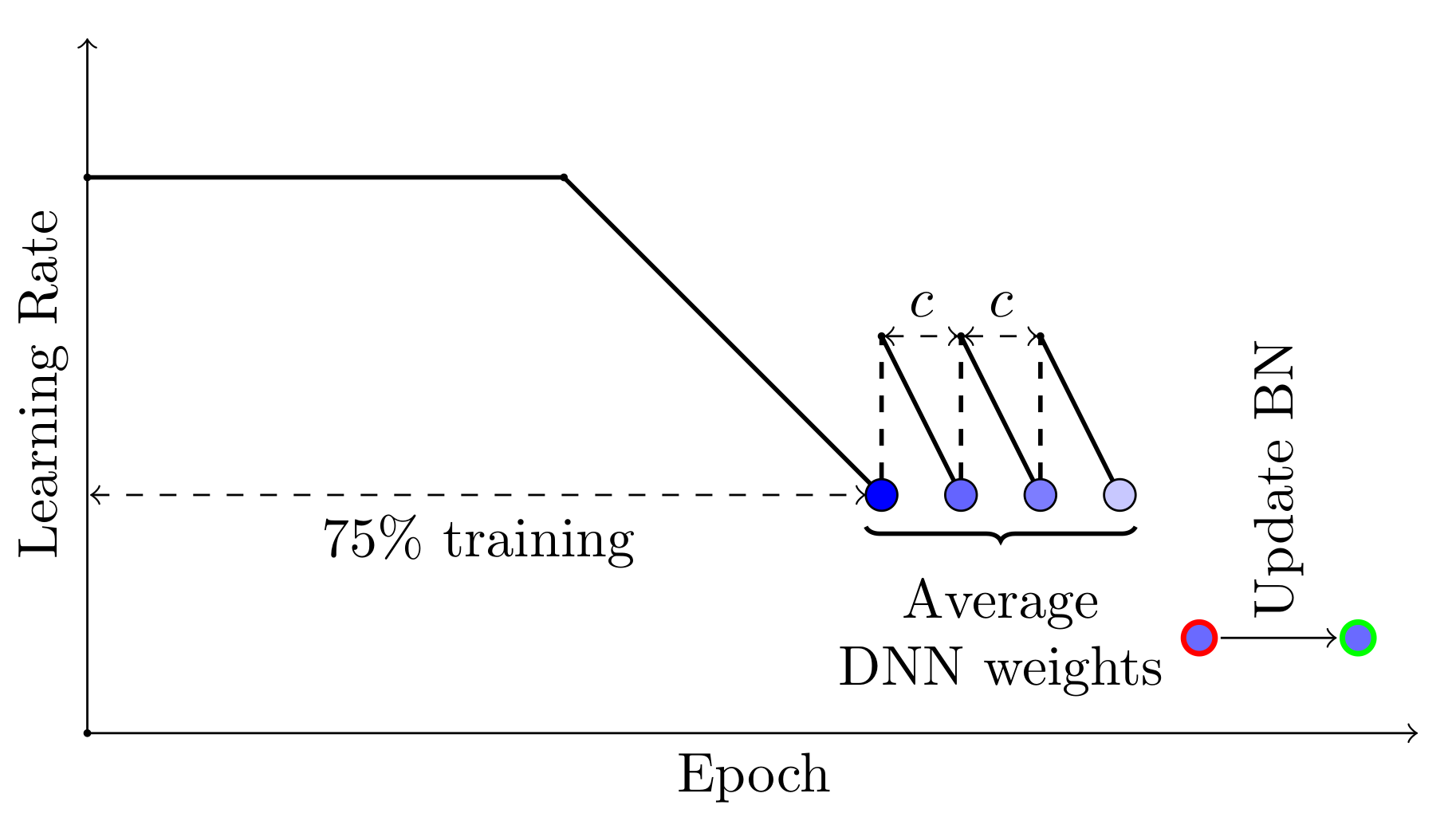
图 3. SWA 的替代学习率计划的示意图。在训练的最后 25%采用周期性学习率,并在每个周期的末尾收集平均模型。
在我们的实现中,您可以通过使用 SWA 在手动模式下实现自定义学习率和权重平均策略。以下代码与本文开头展示的自动模式代码等效。
opt = torchcontrib.optim.SWA(base_opt)
for i in range(100):
opt.zero_grad()
loss_fn(model(input), target).backward()
opt.step()
if i > 10 and i % 5 == 0:
opt.update_swa()
opt.swap_swa_sgd()
在手动模式下,您不指定 swa_start 、 swa_lr 和 swa_freq ,只需在需要更新 SWA 运行平均值时调用 opt.update_swa() (例如在每个学习率周期结束时)。在手动模式下, SWA 不会改变学习率,因此您可以像使用任何其他 torch.optim.Optimizer 一样使用任何您想要的计划。
为什么它会起作用?
SGD 收敛到损失的一个宽广平坦区域内的解。权重空间是极其高维的,平坦区域的体积大部分集中在边界附近,因此 SGD 解总是在损失平坦区域的边界附近找到。另一方面,SWA 平均多个 SGD 解,这使得它可以向平坦区域的中心移动。
我们期望位于损失平坦区域的解决方案比那些靠近边界的解决方案泛化能力更好。事实上,训练和测试误差表面在权重空间中并不完全对齐。位于平坦区域中心的解决方案不像靠近边界的解决方案那样容易受到训练和测试误差表面之间变化的影响。如图 4 所示,我们展示了连接 SWA 和 SGD 解决方案方向的训练损失和测试误差表面。如图所示,虽然 SWA 解决方案的训练损失比 SGD 解决方案高,但它位于低损失区域,并且测试误差显著更好。
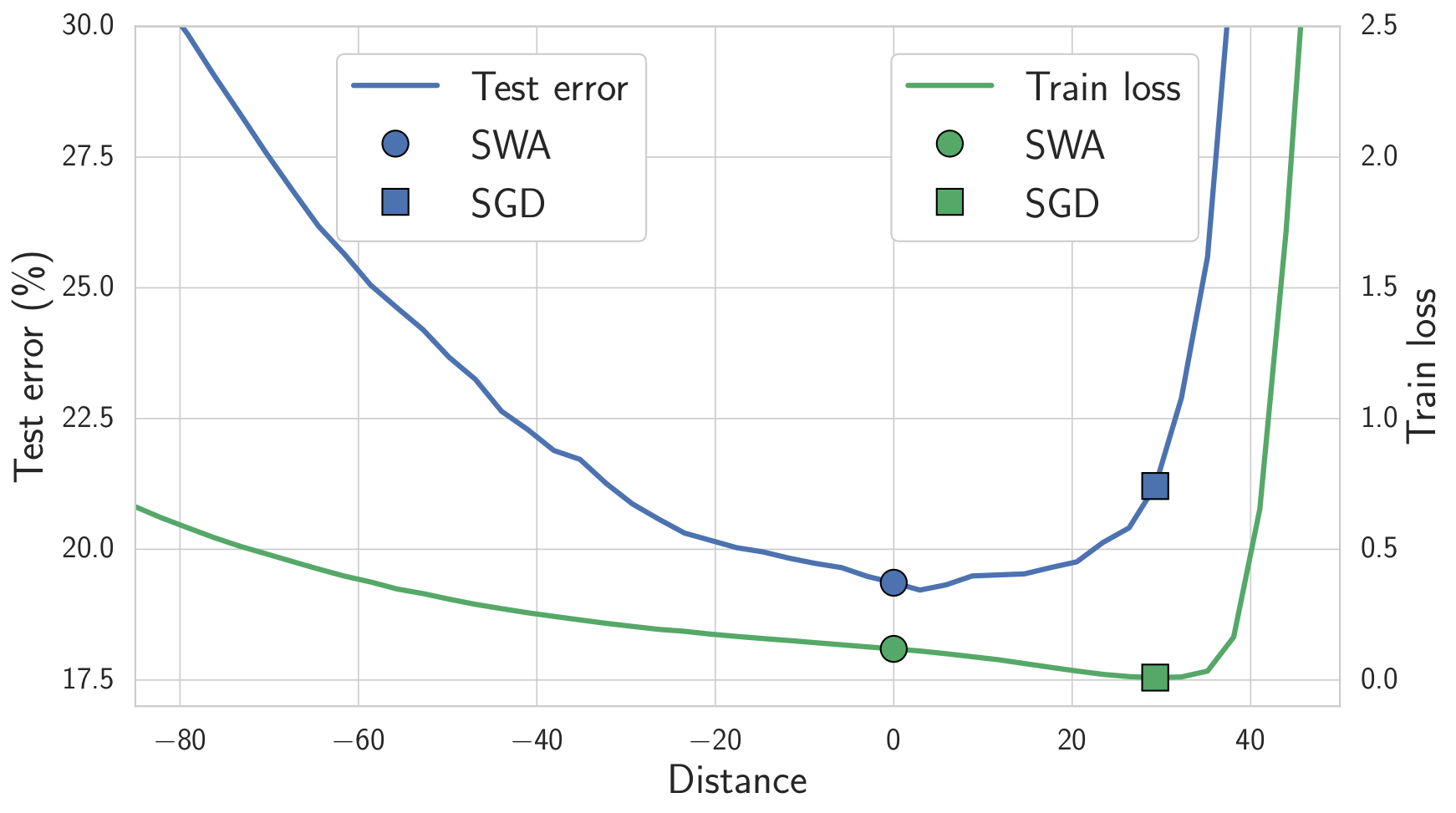
图 4. 连接 SWA 解决方案(圆圈)和 SGD 解决方案(正方形)的线上的训练损失和测试误差。SWA 解决方案位于一个宽泛的低训练损失区域,而 SGD 解决方案位于边界附近。由于训练损失和测试误差表面之间的偏移,SWA 解决方案导致更好的泛化。
例子和结果
我们在这里发布了一个 GitHub 仓库,其中包含使用 torchcontrib 实现 SWA 训练 DNN 的示例。例如,这些示例可以用于在 CIFAR-100 上实现以下结果:
| DNN(预算) | SGD | SWA 1 预算 | SWA 1.25 预算 | SWA 1.5 预算 |
|---|---|---|---|---|
| VGG16(200) | 72.55 ± 0.10 | 73.91 ± 0.12 | 74.17 ± 0.15 | 74.27 ± 0.25 |
| PreResNet110(150) | 76.77 ± 0.38 | 78.75 ± 0.16 | 78.91 ± 0.29 | 79.10 ± 0.21 |
| PreResNet164(150) | 78.49 ± 0.36 | 79.77 ± 0.17 | 80.18 ± 0.23 | 80.35 ± 0.16 |
| WideResNet28x10 (200) | 80.82 ± 0.23 | 81.46 ± 0.23 | 81.91 ± 0.27 | 82.15 ± 0.27 |
半监督学习
在后续论文中,SWA 被应用于半监督学习,并在多个设置中展示了优于已报道最佳结果的改进。例如,使用 SWA,如果您只有 4k 个训练数据点的训练标签,就可以在 CIFAR-10 上获得 95%的准确率(该问题的先前最佳报道结果是 93.7%)。本文还探讨了在 epochs 内多次平均,这可以加速收敛并在给定时间内找到更平缓的解。
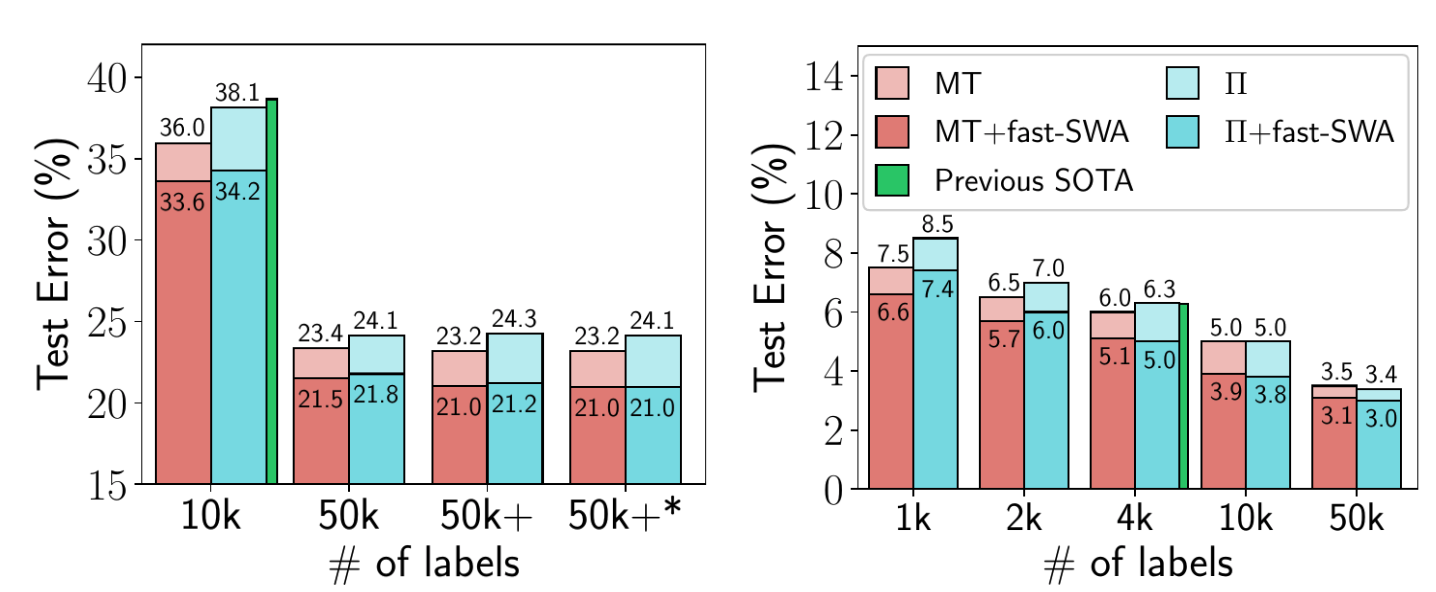
图 5. fast-SWA 在 CIFAR-10 半监督学习中的性能。fast-SWA 在考虑的每个设置中都实现了创纪录的结果。
校准和不确定性估计
SWA-Gaussian(SWAG)是一种简单、可扩展且方便的不确定性估计和贝叶斯深度学习校准方法。与 SWA 类似,SWA 维护 SGD 迭代的运行平均值,SWAG 估计迭代的第一个和第二个矩来构建权重上的高斯分布。SWAG 分布近似了真实后验的形状:图 6 显示了 SWAG 分布位于 CIFAR-100 上 PreResNet-164 的后验对数密度之上。
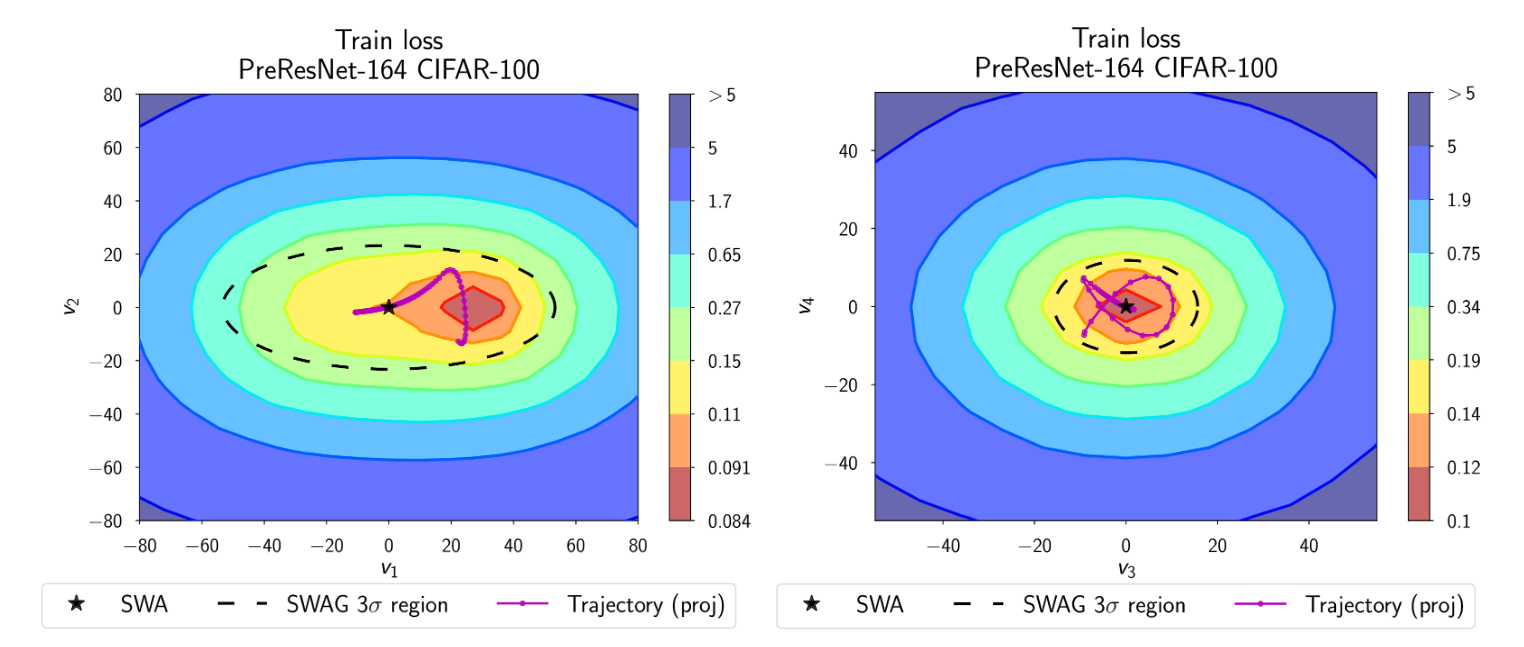
图 6. SWAG 分布位于 CIFAR-100 上 PreResNet-164 的后验对数密度之上。SWAG 分布的形状与后验对齐。
从经验上看,SWAG 在不确定性量化、分布外检测、校准和计算机视觉任务中的迁移学习方面,与 MC dropout、KFAC Laplace 和温度缩放等流行方法相比,表现相当或更好。SWAG 的代码在此处可用。
强化学习
在另一篇后续论文中,SWA 被证明可以提升策略梯度方法 A2C 和 DDPG 在多个 Atari 游戏和 MuJoCo 环境中的性能。
| 环境 | A2C | A2C + SWA |
|---|---|---|
| 破碎 | 522 ± 34 | 703 ± 60 |
| Qbert | 18777 ± 778 | 21272 ± 655 |
| 空中大战 | 7727 ± 1121 | 21676 ± 8897 |
| 海神 | 1779 ± 4 | 1795 ± 4 |
| 疯狂攀爬者 | 147030 ± 10239 | 139752 ± 11618 |
| 飞马骑士 | 9999 ± 402 | 11321 ± 1065 |
低精度训练
我们可以通过结合向下取整的权重和向上取整的权重来过滤量化噪声。此外,通过平均权重以找到损失表面的平坦区域,权重的较大扰动不会影响解的质量(见图 7 和 8)。最近的研究表明,通过将 SWA 应用于低精度设置,在一种称为 SWALP 的方法中,即使所有训练都在 8 位进行,也可以匹配全精度 SGD 的性能[5]。这是一个相当重要的实际结果,因为(1)8 位 SGD 训练的性能明显低于全精度 SGD,并且(2)低精度训练比训练后的低精度预测(通常设置)要困难得多。例如,在 CIFAR-100 上使用浮点(16 位)SGD 训练的 ResNet-164 达到 22.2%的错误率,而 8 位 SGD 达到 24.0%的错误率。相比之下,使用 8 位训练的 SWALP 达到 21.8%的错误率。
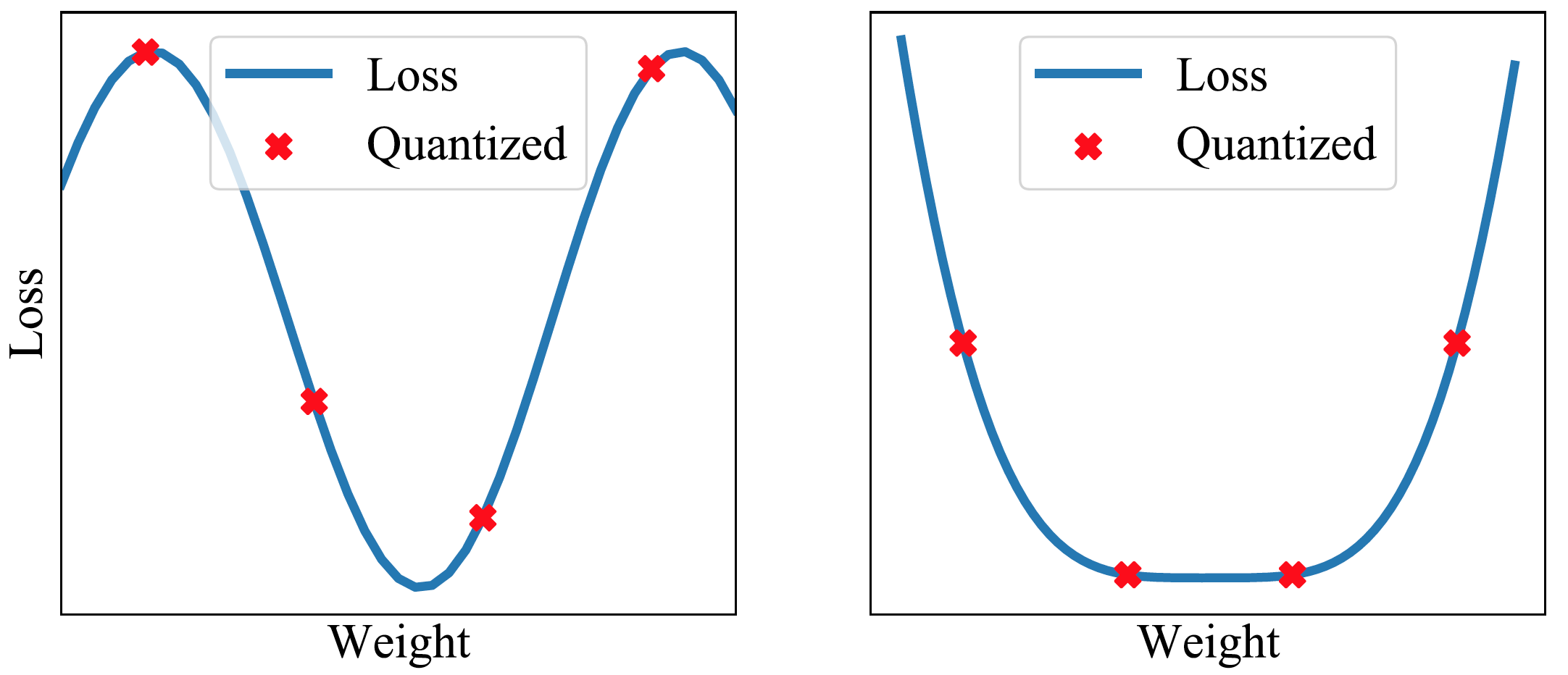
图 7. 在平坦区域进行量化仍然可以提供低损失的解。
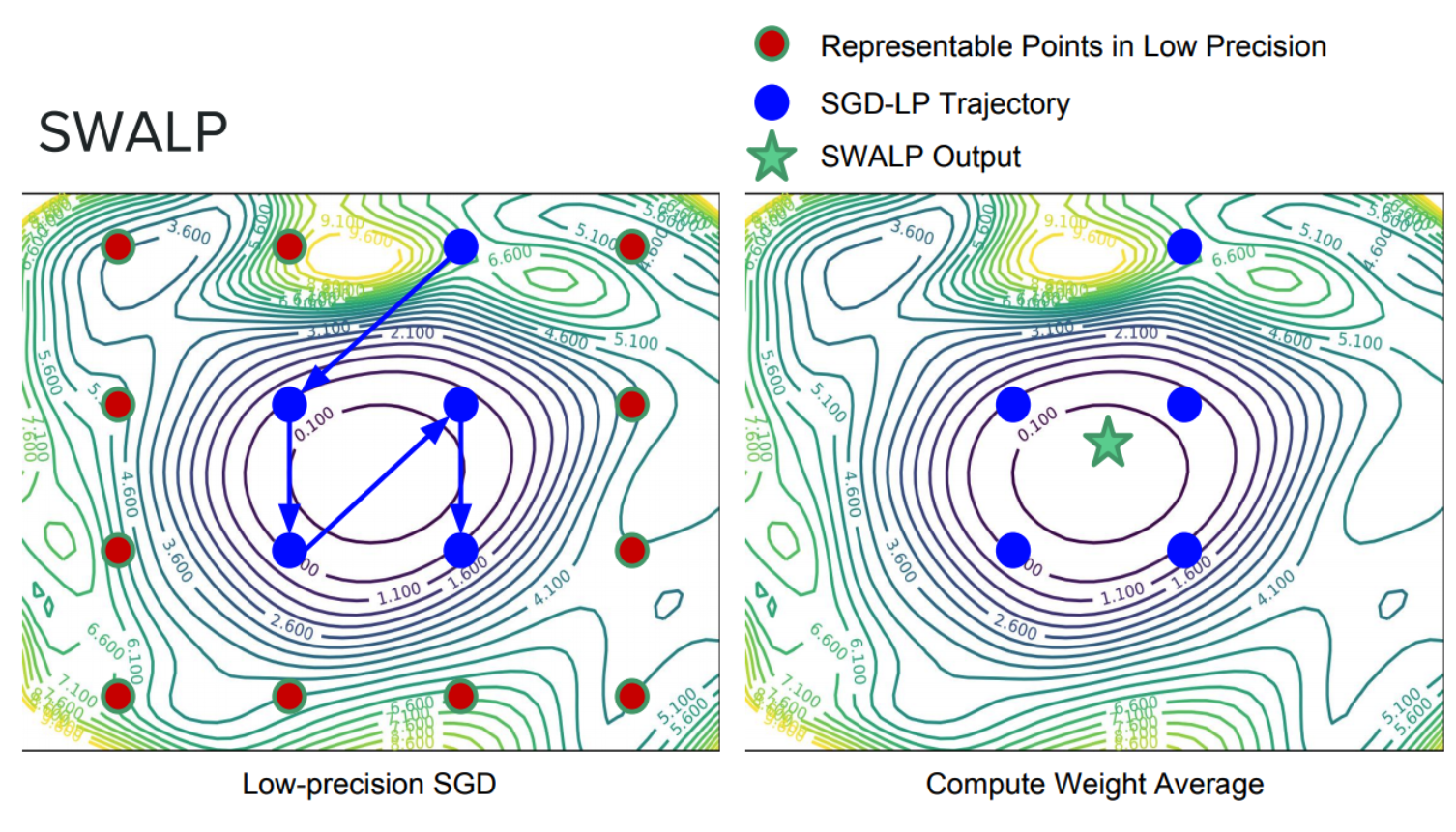
图 8.低精度 SGD 训练(带修改的学习率计划)和 SWALP。
结论
深度学习中最大的未解之谜之一是,为什么 SGD 能够在训练目标高度多模态的情况下找到好的解,因为原则上存在许多参数设置,这些设置可以实现无训练损失但泛化性能差。通过理解与泛化相关的几何特征,如平坦度,我们可以开始解决这些问题,并构建提供更好泛化以及许多其他有用特性的优化器,例如不确定性表示。我们提出了 SWA,这是一种简单的标准 SGD 替代方案,原则上可以惠及任何正在训练深度神经网络的个人。SWA 已在多个领域显示出强大的性能,包括计算机视觉、半监督学习、强化学习、不确定性表示、校准、贝叶斯模型平均和低精度训练。
我们鼓励您尝试使用 SWA!使用 SWA 现在与使用 PyTorch 中的任何其他优化器一样简单。即使您已经使用 SGD(或任何其他优化器)训练了您的模型,通过从预训练模型开始运行 SWA 进行少量 epoch,也非常容易实现 SWA 的好处。
- [1] 平均权重导致更宽的优化范围和更好的泛化;帕维尔·伊兹梅洛夫,德米特里·波多普里欣,蒂穆尔·加里波夫,德米特里·维特罗夫,安德鲁·戈登·威尔逊;人工智能中的不确定性(UAI),2018
- [2] 对于未标记数据有许多一致的解释:为什么你应该平均;本·阿蒂瓦拉特昆,马克·芬齐,帕维尔·伊兹梅洛夫,安德鲁·戈登·威尔逊;国际学习表示会议(ICLR),2019
- [3] 使用权重平均提高深度强化学习中的稳定性;叶夫根尼·尼基申,帕维尔·伊兹梅洛夫,本·阿蒂瓦拉特昆,德米特里·波多普里欣,蒂穆尔·加里波夫,帕维尔·谢韦奇科夫,德米特里·维特罗夫,安德鲁·戈登·威尔逊,UAI 2018 研讨会:深度学习中的不确定性,2018
- [4] 深度学习中贝叶斯不确定性的简单基线,Wesley Maddox,Timur Garipov,Pavel Izmailov,Andrew Gordon Wilson,arXiv 预印本,2019:https://arxiv.org/abs/1902.02476
- [5] SWALP:低精度训练中的随机权重平均,Guandao Yang,Tianyi Zhang,Polina Kirichenko,Junwen Bai,Andrew Gordon Wilson,Christopher De Sa,即将发表在国际机器学习大会上(ICML),2019。
- [6] David Ruppert. 从缓慢收敛的 Robbins-Monro 过程中进行有效估计。技术报告,康奈尔大学运筹学与工业工程系,1988。
- [7] 通过平均加速随机逼近。Boris T Polyak 和 Anatoli B Juditsky。SIAM 控制与优化杂志,30(4):838–855,1992。
- [8] 损失曲面、模式连通性和深度神经网络快速集成,Timur Garipov,Pavel Izmailov,Dmitrii Podoprikhin,Dmitry Vetrov,Andrew Gordon Wilson。神经信息处理系统(NeurIPS),2018