您使用随机梯度下降(SGD)还是 Adam?无论您使用什么方法来训练您的神经网络,您都可以通过一种简单的新技术显著提高泛化能力,而几乎无需额外成本。这种新技术现在在 PyTorch 1.6 中原生支持,称为随机权重平均(SWA)[1]。即使您已经训练了您的模型,也可以通过从预训练模型开始运行 SWA 几个 epoch 来轻松实现 SWA 的好处。一次又一次,研究人员发现,SWA 在几乎无需额外成本或努力的情况下,可以显著提高各种实际应用中调优良好的模型的性能!
SWA 具有广泛的应用和功能:
- 与标准训练技术相比,SWA 在计算机视觉(例如,在 ImageNet 和 CIFAR 基准测试上的 VGG、ResNets、Wide ResNets 和 DenseNets)中显著提高了性能[1, 2]。
- SWA 在半监督学习和领域自适应的关键基准测试中提供了最先进的性能[2]。
- SWA 已被证明可以提高语言模型(例如,AWD-LSTM 在 WikiText-2[4]上)和深度强化学习中的策略梯度方法的表现[3]。
- SWA 的扩展 SWAG 可以在贝叶斯深度学习中近似贝叶斯模型平均,并在各种设置中实现了最先进的不确定性校准结果。此外,其最近推广的 MultiSWAG 提供了显著的额外性能提升,并缓解了双重下降[4, 10]。另一种方法,子空间推理,在 SWA 解附近的参数空间的小子空间中近似贝叶斯后验[5]。
- SWA 用于低精度训练的 SWALP 可以匹配全精度 SGD 训练的性能,即使所有数字都量化到 8 位,包括梯度累加器[6]。
- SWA 并行,SWAP,通过使用大批量训练显著加速了神经网络的训练,特别是在 CIFAR-10 上训练神经网络达到 94%的准确率,创下了 27 秒的记录[11]。
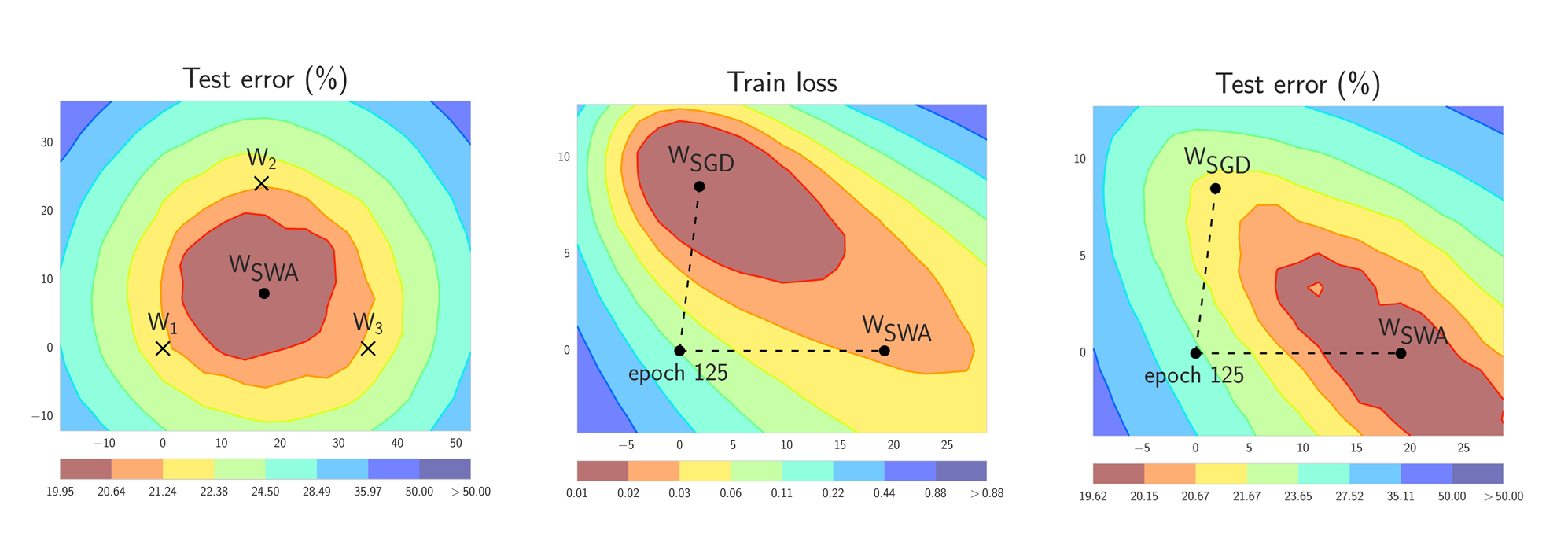
图 1. SWA 和 SGD 在 CIFAR-100 上的 Preactivation ResNet-164 的示意图[1]。左:三个 FGE 样本的测试误差表面和相应的 SWA 解(在权重空间中平均)。中间和右:测试误差和训练损失表面,显示了 SGD(在收敛时)和 SWA 的权重,它们从 SGD 相同的初始化开始,经过 125 个训练周期。请参阅[1]了解这些图是如何构建的。
简而言之,SWA 通过修改学习率计划(见图 1 的左侧面板)对 SGD(或任何随机优化器)遍历的权重进行等平均。SWA 解最终位于损失宽平区域的中心,而 SGD 倾向于收敛到低损失区域的边界,这使得它容易受到训练和测试误差表面之间的偏移的影响(见图 1 的中间和右面板)。我们强调,SWA 可以与任何优化器一起使用,如 Adam,并且不特定于 SGD。
之前,SWA 位于 PyTorch contrib 中。在 PyTorch 1.6 版本中,我们提供了一个新的便捷的 SWA 实现,位于 torch.optim.swa_utils 中。
这只是平均 SGD 吗?
从高层次来看,平均 SGD 迭代的历史可以追溯到几十年前的凸优化[7, 8],有时也被称为 Polyak-Ruppert 平均或平均 SGD。但细节很重要。平均 SGD 通常与递减的学习率以及指数移动平均(EMA)结合使用,通常用于凸优化。在凸优化中,重点是提高收敛速度。在深度学习中,这种形式的平均 SGD 平滑了 SGD 迭代的轨迹,但与 SGD 并没有太大的区别。
相比之下,SWA 使用等权重的 SGD 迭代平均值,并采用修改后的周期性或高常量学习率,利用深度学习特有的训练目标平坦性[8],以改善泛化能力。
随机权重平均化是如何工作的?
使 SWA 工作有两个重要的因素。首先,SWA 使用修改后的学习率计划,使得 SGD(或 Adam 等其他优化器)继续在最优解周围弹跳并探索不同的模型,而不是简单地收敛到单个解。例如,我们可以在前 75%的训练时间内使用标准的衰减学习率策略,然后为剩余的 25%时间设置一个合理的高常数值(见图 2)。第二个因素是对 SGD 遍历的网络的权重(通常是等权重的平均)进行平均。例如,我们可以在训练的最后 25%时间内,在每个 epoch 结束时维护一个权重的运行平均值(见图 2)。训练完成后,我们将网络的权重设置为计算出的 SWA 平均值。
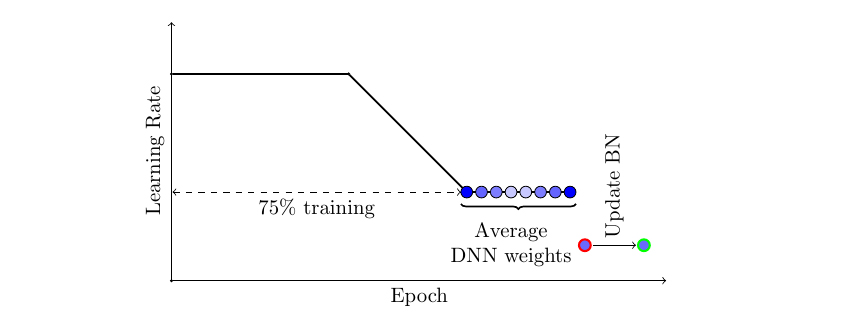
图 2. SWA 采用的学习率计划的示意图。前 75%的训练使用标准衰减计划,然后剩余 25%使用高常数值。SWA 平均值在训练的最后 25%时间内形成。
一个重要的细节是批量归一化。批量归一化层在训练过程中计算激活的运行统计。请注意,SWA 权重的平均值在训练过程中永远不会用于预测。因此,批量归一化层在训练结束时没有计算激活统计。我们可以通过使用 SWA 模型在训练数据上执行单个前向传递来计算这些统计信息。
虽然我们在上面的描述中为了简单起见关注了 SGD,但 SWA 可以与任何优化器结合使用。您还可以使用周期性学习率而不是高常数值(例如,参见[2])。
如何在 PyTorch 中使用 SWA?
在 torch.optim.swa_utils 中,我们实现了所有 SWA 组件,以便方便地将 SWA 与任何模型一起使用。特别是,我们实现了 AveragedModel SWA 模型类、 SWALR 学习率调度器和 update_bn 更新 SWA 批量归一化统计信息的实用函数。
在下面的示例中, swa_model 是一个累积权重平均值的 SWA 模型。我们总共训练该模型 300 个 epoch,并在第 160 个 epoch 切换到 SWA 学习率计划,并开始收集 SWA 参数的平均值。
from torch.optim.swa_utils import AveragedModel, SWALR
from torch.optim.lr_scheduler import CosineAnnealingLR
loader, optimizer, model, loss_fn = ...
swa_model = AveragedModel(model)
scheduler = CosineAnnealingLR(optimizer, T_max=100)
swa_start = 5
swa_scheduler = SWALR(optimizer, swa_lr=0.05)
for epoch in range(100):
for input, target in loader:
optimizer.zero_grad()
loss_fn(model(input), target).backward()
optimizer.step()
if epoch > swa_start:
swa_model.update_parameters(model)
swa_scheduler.step()
else:
scheduler.step()
# Update bn statistics for the swa_model at the end
torch.optim.swa_utils.update_bn(loader, swa_model)
# Use swa_model to make predictions on test data
preds = swa_model(test_input)
接下来,我们将详细解释 torch.optim.swa_utils 的每个组件。
AveragedModel 类用于计算 SWA 模型的权重。您可以通过运行 swa_model = AveragedModel(model) 创建一个平均模型。然后,您可以通过 swa_model.update_parameters(model) 更新平均模型的参数。默认情况下, AveragedModel 计算您提供的参数的运行等平均值,但您也可以使用自定义平均函数通过 avg_fn 参数。在以下示例中, ema_model 计算指数移动平均值。
ema_avg = lambda averaged_model_parameter, model_parameter, num_averaged:\
0.1 * averaged_model_parameter + 0.9 * model_parameter
ema_model = torch.optim.swa_utils.AveragedModel(model, avg_fn=ema_avg)
在实践中,我们发现与图 2 中修改后的学习率计划一起使用的等平均值提供了最佳性能。
SWALR 是一个学习率调度器,将学习率逐渐降低到一个固定值,然后保持不变。例如,以下代码创建了一个调度器,将学习率从初始值线性降低到 0.05 ,在 5 个 epochs 内对每个参数组进行操作。
swa_scheduler = torch.optim.swa_utils.SWALR(optimizer,
anneal_strategy="linear", anneal_epochs=5, swa_lr=0.05)
我们还实现了将学习率逐渐降低到一个固定值( anneal_strategy="cos" )的余弦衰减。在实践中,我们通常在 swa_start 个 epochs 时切换到 SWALR (例如,在训练 epochs 的 75%之后),并同时开始计算权重的运行平均值:
scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=100)
swa_start = 75
for epoch in range(100):
# <train epoch>
if i > swa_start:
swa_model.update_parameters(model)
swa_scheduler.step()
else:
scheduler.step()
最后, update_bn 是一个计算给定数据加载器 loader 上 SWA 模型批归一化统计信息的工具函数:
torch.optim.swa_utils.update_bn(loader, swa_model)
update_bn 将 swa_model 应用于数据加载器中的每个元素,并计算模型中每个批归一化层的激活统计信息。
一旦计算了 SWA 平均值并更新了批量归一化层,您就可以应用 swa_model 来对测试数据进行预测。
为什么它会起作用?
损失表面存在大面积的平坦区域[9]。如图 3 所示,我们在参数空间的一个子空间中展示了损失表面的可视化,该子空间包含连接两个独立训练的 SGD 解的路径,路径上的每个点损失都相对较低。SGD 在这些区域的边界附近收敛,因为内部几乎没有梯度信号可以移动,因为该区域的所有点都具有相似的损失值。通过增加学习率,SWA 在这个平坦区域周围旋转,然后通过平均迭代值,向平坦区域的中心移动。
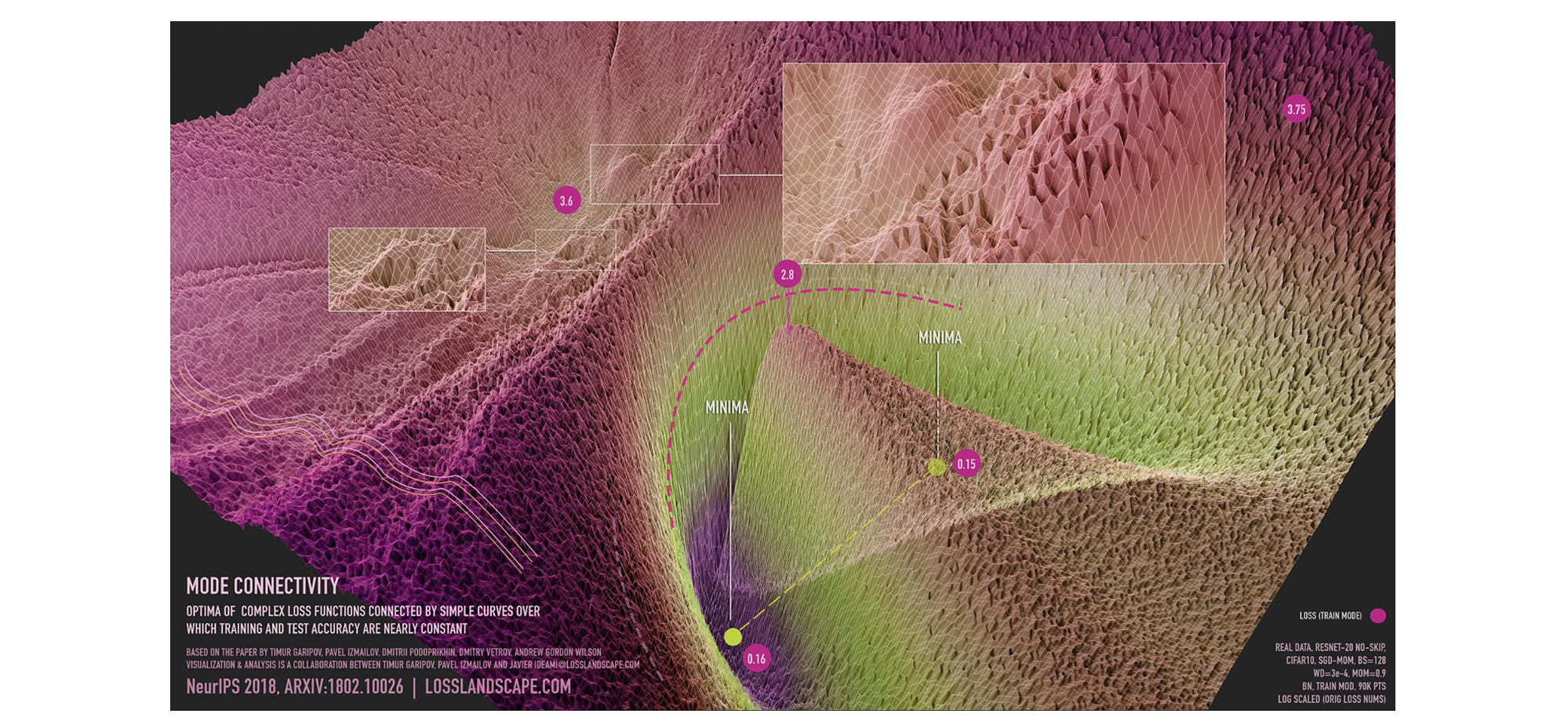
图 3:ResNet-20 在 CIFAR-10 数据集上无跳跃连接的模式连通性可视化。该可视化与 Javier Ideami(https://losslandscape.com/)合作完成。更多详情请参阅这篇博客文章。
我们期望位于损失平坦区域的解决方案比靠近边界的解决方案泛化能力更好。事实上,训练和测试误差曲面在权重空间中并不完全对齐。位于平坦区域的解决方案不像靠近边界的解决方案那样容易受到训练和测试误差曲面之间差异的影响。如图 4 所示,我们展示了连接 SWA 和 SGD 解决方案方向的训练损失和测试误差曲面。如图所示,虽然 SWA 解决方案的训练损失比 SGD 解决方案高,但它位于一个低损失的区域,并且测试误差显著更好。
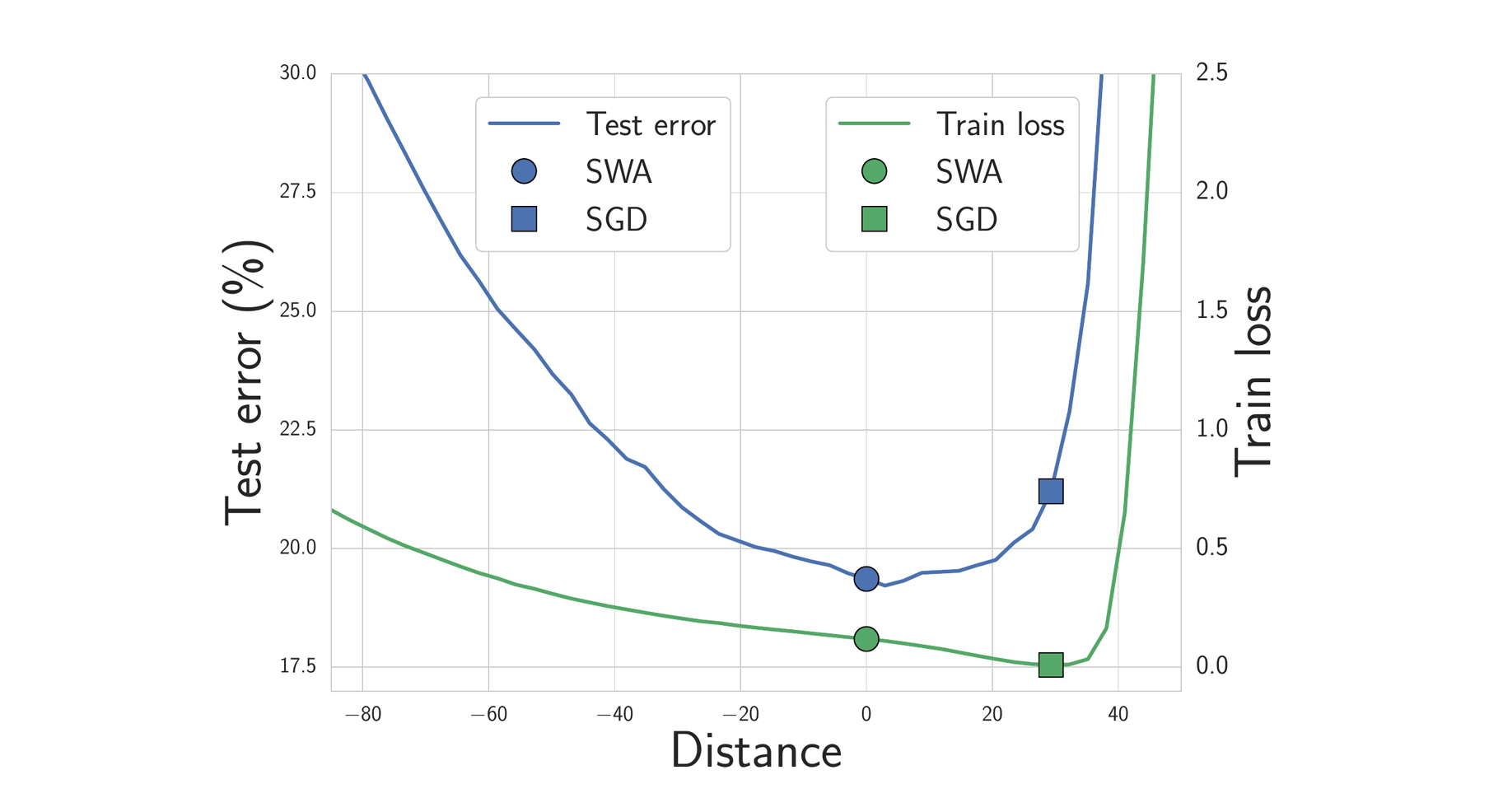
图 4. 连接 SWA 解决方案(圆圈)和 SGD 解决方案(正方形)的线上的训练损失和测试误差。SWA 解决方案位于一个宽泛的低训练损失区域,而 SGD 解决方案位于边界附近。由于训练损失和测试误差曲面之间的差异,SWA 解决方案导致更好的泛化。
SWA 取得了哪些成果?
我们发布了一个包含使用 PyTorch 实现 SWA 训练 DNNs 示例的 GitHub 仓库。例如,这些示例可以用于在 CIFAR-100 上实现以下结果:
| VGG-16 | ResNet-164 | WideResNet-28x10 | |
|---|---|---|---|
| SGD | 72.8 ± 0.3 | 78.4 ± 0.3 | 81.0 ± 0.3 |
| SWA | 74.4 ± 0.3 | 79.8 ± 0.4 | 82.5 ± 0.2 |
半监督学习
在后续论文中,SWA 被应用于半监督学习,在多个设置中提高了最佳报道结果[2]。例如,如果您只有 4k 个训练数据点的训练标签,使用 SWA 可以在 CIFAR-10 上获得 95%的准确率(该问题的先前最佳报道结果是 93.7%)。本文还探讨了在 epochs 内多次平均,这可以加速收敛并在给定时间内找到更平缓的解。
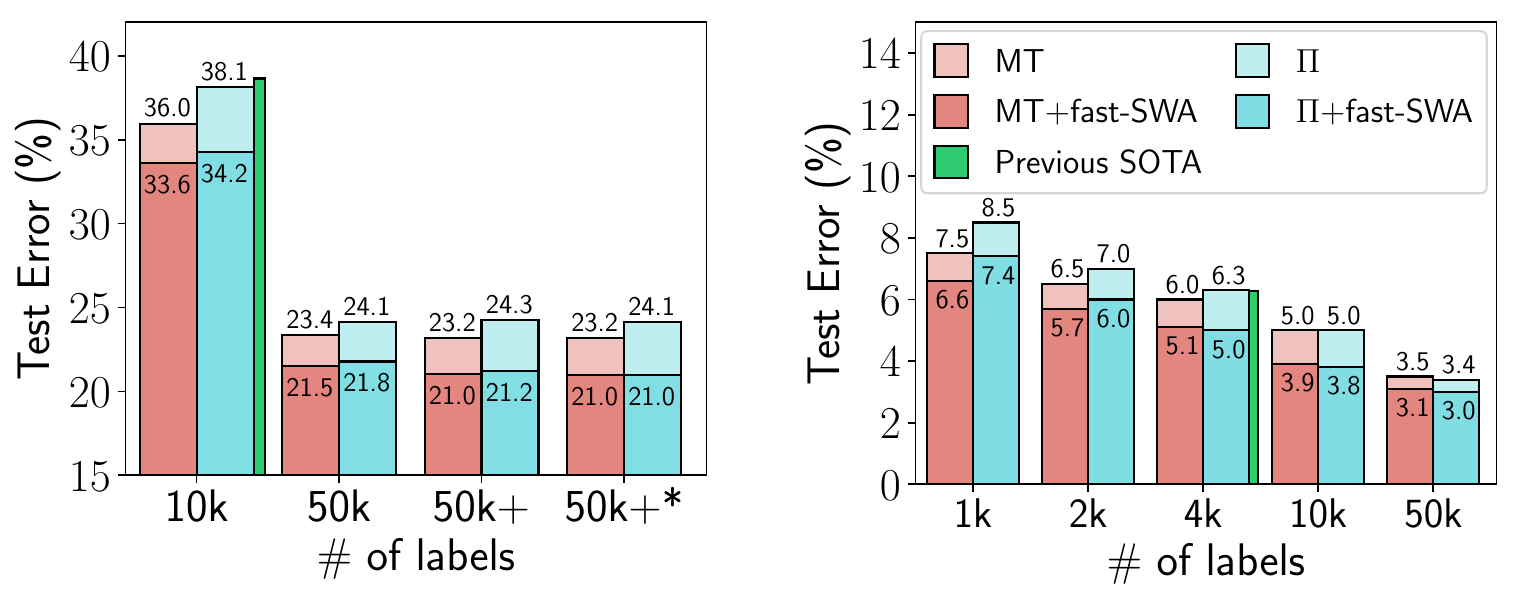
图 5. fast-SWA 在 CIFAR-10 半监督学习中的性能。fast-SWA 在考虑的每个设置中都实现了创纪录的结果。
强化学习
在另一篇后续论文中,SWA 被证明可以改善策略梯度方法 A2C 和 DDPG 在多个 Atari 游戏和 MuJoCo 环境中的性能[3]。这种应用也是 SWA 与 Adam 一起使用的实例。回想一下,SWA 并不特定于 SGD,几乎可以给任何优化器带来好处。
| 环境名称 | A2C | A2C + SWA |
|---|---|---|
| 破碎 | 522 ± 34 | 703 ± 60 |
| Qbert | 18777 ± 778 | 21272 ± 655 |
| 空中大战 | 7727 ± 1121 | 21676 ± 8897 |
| 海神 | 1779 ± 4 | 1795 ± 4 |
| 飞马骑士 | 9999 ± 402 | 11321 ± 1065 |
| 疯狂攀爬者 | 147030 ± 10239 | 139752 ± 11618 |
低精度训练
我们可以通过结合向下舍入的权重和向上舍入的权重来过滤量化噪声。此外,通过平均权重以找到损失表面的平坦区域,权重的较大扰动不会影响解的质量(见图 9 和图 10)。最近的研究表明,通过将 SWA 应用于低精度设置,在一种称为 SWALP 的方法中,即使所有训练都在 8 位进行,也可以匹配全精度 SGD 的性能[5]。这是一个相当重要的实际结果,因为(1)8 位 SGD 训练的性能明显低于全精度 SGD,并且(2)低精度训练比训练后的低精度预测(通常设置)要困难得多。例如,使用浮点(16 位)SGD 在 CIFAR-100 上训练的 ResNet-164 达到 22.2%的错误率,而 8 位 SGD 达到 24.0%的错误率。相比之下,8 位训练的 SWALP 达到 21.8%的错误率。
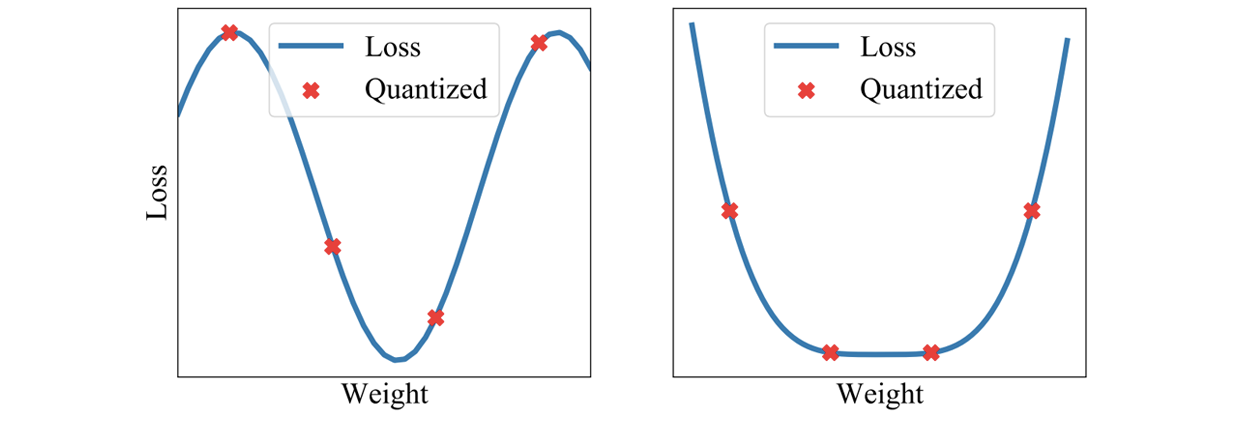
图 9.对解决方案进行量化会导致权重的扰动,与宽解决方案(右侧)相比,对锐利解决方案(左侧)的质量影响更大。
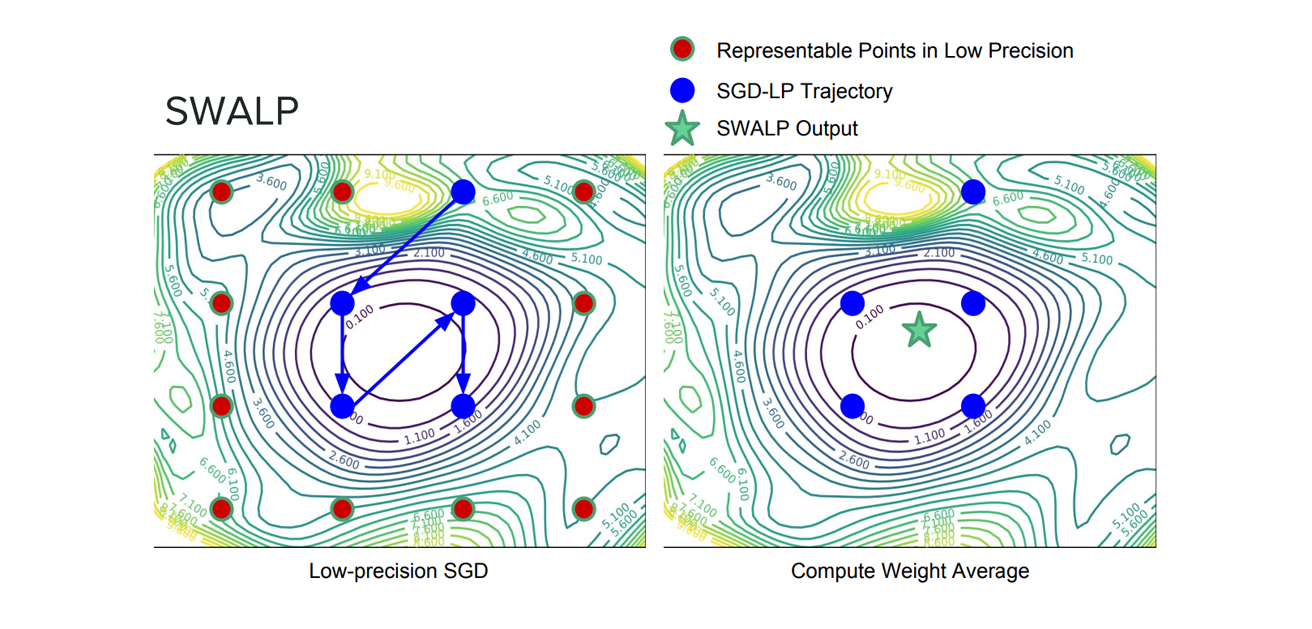
图 10.标准低精度训练与 SWALP 之间的差异。
另一项工作,SQWA,提出了一种用于低精度神经网络量化和微调的方法[12]。特别是,SQWA 在 CIFAR-100 和 ImageNet 上对量化为 2 位的 DNN 实现了最先进的结果。
校准和不确定性估计
通过在损失函数中找到一个中心解,SWA 还可以提高校准和不确定性表示。事实上,SWA 可以看作是对集成的一种近似,类似于贝叶斯模型平均,但只有一个模型[1]。
SWA 可以看作是使用修改后的学习率计划对 SGD 迭代的首次矩进行操作。我们可以通过也取迭代的二次矩来形成关于权重的高斯近似后验,进一步用 SGD 迭代来表征损失几何。这种方法,SWA-Gaussian(SWAG)是一种简单、可扩展且方便的不确定性估计和贝叶斯深度学习中的校准方法[4]。SWAG 分布近似了真实后验的形状:图 6 显示了 SWAG 分布和 ResNet-20 在 CIFAR-10 上的后验对数密度。

图 6. SWAG 后验近似和 ResNet-20(无跳跃连接)在 CIFAR-10 数据集上训练的损失表面,该训练在 SWAG 协方差矩阵的两个最大特征值形成的子空间中进行。SWAG 分布的形状与后验对齐:两个分布的峰值重合,且两个分布在一个方向上的宽度大于正交方向。可视化与 Javier Ideami 合作完成。
从经验上看,SWAG 在不确定性量化、分布外检测、校准和计算机视觉任务中的迁移学习方面,与 MC dropout、KFAC Laplace 和温度缩放等流行方法相比,表现相当或更好。SWAG 的代码在此处可用。
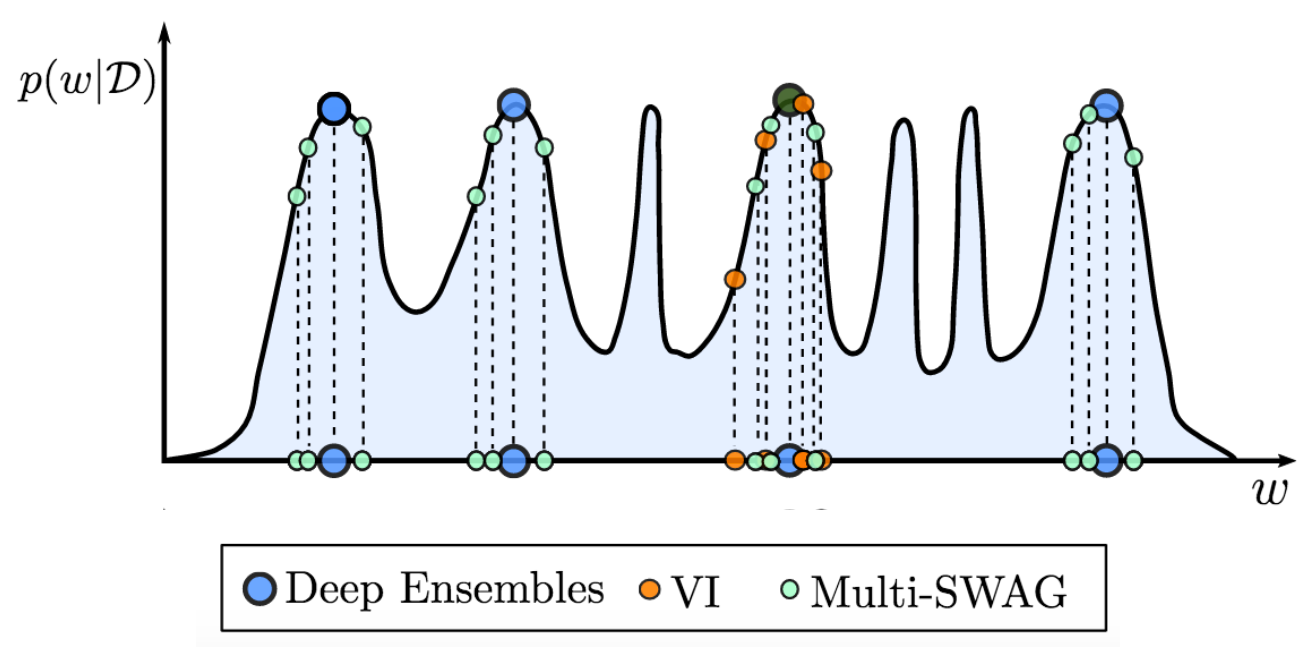
图 7. MultiSWAG 扩展了 SWAG 和深度集成,以在多个吸引子中进行贝叶斯模型平均,从而显著提高性能。相比之下,如图所示,深度集成选择不同的模式,而标准变分推断(VI)在单个吸引子内进行边缘化(模型平均)。
MultiSWAG [9] 使用多个独立的 SWAG 模型来形成高斯混合作为近似后验分布。不同的吸引子包含对数据高度互补的解释。因此,对这些多个吸引子进行边缘化可以显著提高准确性和不确定性表示。MultiSWAG 可以被视为深度集成的推广,但性能有所提升。
事实上,我们在图 8 中看到,MultiSWAG 完全缓解了双重下降——更灵活的模型性能单调提高——并且比 SGD 提供了显著改进的泛化能力。例如,当 ResNet-18 的宽度为 20 层时,Multi-SWAG 实现的错误率低于 30%,而 SGD 实现的错误率超过 45%,差距超过 15%!
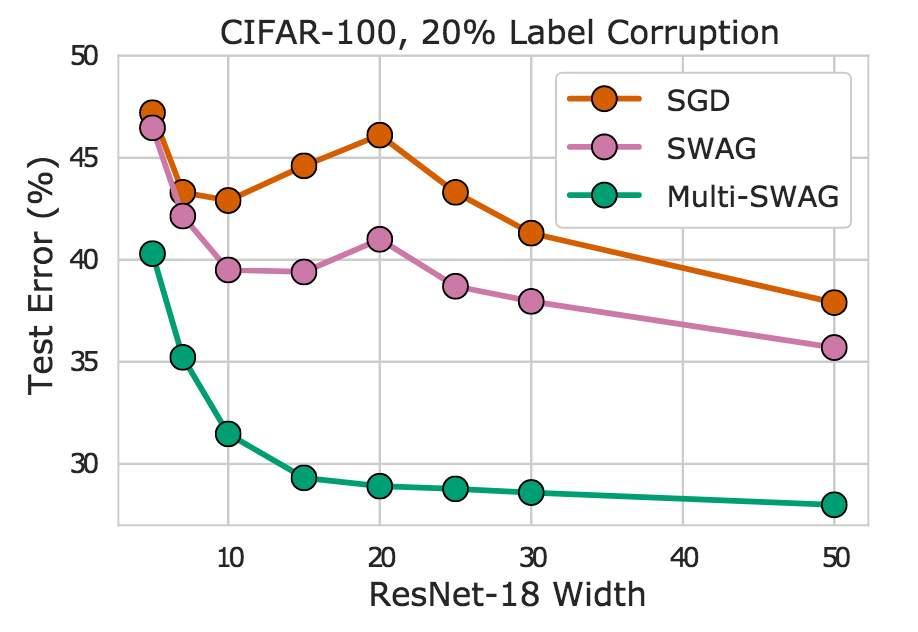
图 8. SGD、SWAG 和 MultiSWAG 在 CIFAR-100 上对 ResNet-18 不同宽度的比较。我们看到 MultiSWAG 特别缓解了双重下降,并在 SGD 上提供了显著的准确度提升。
参考文献编号[10]也考虑了多 SWA,该算法在集成中使用多个独立训练的 SWA 解决方案,在没有任何额外计算成本的情况下,提供了比深度集成更好的性能。MultiSWA 和 MultiSWAG 的代码在此处可用。
另一种方法,子空间推理,在 SWA 解周围构建一个低维子空间,并消去该子空间中的权重来近似贝叶斯模型平均[5]。子空间推理使用 SGD 迭代的统计信息来构建 SWA 解和子空间。该方法在分类和回归问题中的预测精度和不确定性校准方面都取得了优异的性能。代码在此处可用。
尝试一下!
深度学习中一个最大的未解之谜之一是为什么 SGD 能够在训练目标高度多模态的情况下找到良好的解,因为有许多参数设置可以实现无训练损失但泛化能力差。通过理解与泛化相关的几何特征,如平坦度,我们可以开始解决这些问题,并构建提供更好泛化能力以及许多其他有用特性的优化器,例如不确定性表示。我们提出了 SWA,这是一种简单的标准优化器(如 SGD 和 Adam)的替代品,原则上可以惠及任何正在训练深度神经网络的用户。SWA 已在多个领域显示出强大的性能,包括计算机视觉、半监督学习、强化学习、不确定性表示、校准、贝叶斯模型平均和低精度训练。
我们鼓励您尝试 SWA!现在使用 SWA 与 PyTorch 中的任何标准训练一样简单。即使您已经训练了模型,您也可以通过从预训练模型运行少量 epoch 来使用 SWA 显著提高性能。
[1] 平均权重导致更宽的优化范围和更好的泛化能力;Pavel Izmailov, Dmitry Podoprikhin, Timur Garipov, Dmitry Vetrov, Andrew Gordon Wilson;人工智能中的不确定性(UAI),2018。
[2] 对于未标记数据存在许多一致的解释:为什么你应该平均;Ben Athiwaratkun, Marc Finzi, Pavel Izmailov, Andrew Gordon Wilson;学习表示国际会议(ICLR),2019。
[3] 使用权重平均提高深度强化学习的稳定性;Evgenii Nikishin, Pavel Izmailov, Ben Athiwaratkun, Dmitrii Podoprikhin, Timur Garipov, Pavel Shvechikov, Dmitry Vetrov, Andrew Gordon Wilson;UAI 2018 研讨会:深度学习中的不确定性,2018。
[4] 深度学习中贝叶斯不确定性的简单基线;Wesley Maddox, Timur Garipov, Pavel Izmailov, Andrew Gordon Wilson;神经信息处理系统(NeurIPS),2019。
[5] 子空间推理在贝叶斯深度学习中的应用 萨夫拉·伊兹梅洛夫,韦斯利·马多克斯,波利娜·基里琴科,蒂穆尔·加里波夫,德米特里·韦特罗夫,安德鲁·戈登·威尔逊 不确定性人工智能(UAI),2019。
[6] SWALP:低精度训练中的随机权重平均 阳冠道,张天翼,波利娜·基里琴科,白俊文,安德鲁·戈登·威尔逊,克里斯托弗·德·萨 国际机器学习会议(ICML),2019。
[7] 大卫·鲁珀特。从缓慢收敛的罗宾斯-莫诺过程中进行有效估计 技术报告,康奈尔大学运筹学与工业工程系,1988。
[8] 通过平均加速随机逼近 博里斯·波利亚克和阿纳托利·尤迪茨基;美国工业与应用数学学会控制与优化杂志,第 30 卷第 4 期:838–855,1992。
[9] 深度神经网络快速集成中的损失曲面、模式连通性 Timur Garipov, Pavel Izmailov, Dmitrii Podoprikhin, Dmitry Vetrov, Andrew Gordon Wilson. 神经信息处理系统(NeurIPS),2018。
[10] 贝叶斯深度学习与泛化的概率视角 Andrew Gordon Wilson, Pavel Izmailov. ArXiv 预印本,2020。
[11] 并行中的随机权重平均:泛化良好的大批量训练 Gupta, Vipul, Santiago Akle Serrano, 和 Dennis DeCoste;学习表示国际会议(ICLR),2019。
[12] SQWA:用于提高低精度深度神经网络泛化能力的随机量化权重平均 Shin, Sungho, Yoonho Boo, 和 Wonyong Sung;arXiv 预印本 2020。