Overview of PyTorch Autograd Engine

由 Preferred Networks，Inc.提供

本文基于 PyTorch 版本 1.8 编写，尽管它也适用于较旧版本，因为大部分机制都保持不变。

为了帮助理解这里解释的概念，建议您阅读@ezyang 的出色博客文章：PyTorch 内部结构，如果您不熟悉 PyTorch 架构组件，如 ATen 或 c10d。

什么是 autograd？

背景

PyTorch 通过自动微分计算函数相对于输入的梯度。自动微分是一种技术，给定一个计算图，可以计算输入的梯度。自动微分可以有两种不同的方式；正向模式和反向模式。正向模式意味着我们在计算函数结果的同时计算梯度，而反向模式则需要我们首先评估函数，然后从输出开始计算梯度。虽然两种模式都有其优缺点，但由于输出的数量少于输入的数量，反向模式成为了事实上的选择，这允许更高效的计算。请参阅[3]了解更多信息。

自动微分依赖于经典的微积分公式，即链式法则。链式法则允许我们通过拆分和重新组合来计算非常复杂的导数。

从严格意义上讲，给定一个复合函数 $f(g(x))$ ，我们可以计算其导数为 $\frac{\partial}{\partial x} f(g(x)) = f'(g(x))g'(x)$ 。这个结果使得自动微分得以工作。通过结合组成更大函数（如神经网络）的简单函数的导数，可以计算给定点的梯度确切值，而不是依赖于数值近似，这需要多次扰动输入以获得值。

为了理解逆模式的工作原理，让我们来看一个简单的函数 $f(x, y) = log(x*y)$ 。图 1 显示了其计算图，其中输入 x、y 在左侧，通过一系列操作生成输出 z。

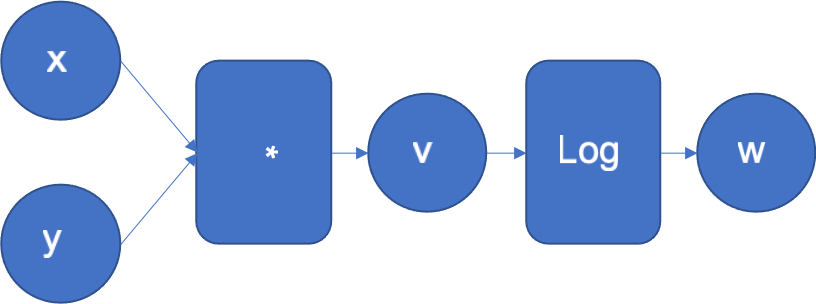
图 1：函数 f(x, y) = log(x*y)的计算图

自动微分引擎通常会执行这个图。它还会扩展它来计算 w 相对于输入 x、y 和中间结果 v 的导数。

示例函数可以被分解为 f 和 g，其中 $f(x, y) = log(g(x, y))$ 和 $g(x, y) = xy$ 。每当引擎在图中执行一个操作时，该操作的导数就会被添加到图中，以便在后续的反向传播中执行。请注意，引擎知道基本函数的导数。

在上述示例中，当将 x 和 y 相乘得到 v 时，引擎将扩展图以使用它已知的乘法导数定义来计算乘法的偏导数。 $\frac{\partial}{\partial x} g(x, y) = y$ 和 $\frac{\partial}{\partial y} g(x, y) = x$ 。扩展后的图如图 2 所示，其中 MultDerivative 节点还通过输入梯度计算结果的梯度乘积以应用链式法则；这将在后续操作中明确看到。请注意，反向图（绿色节点）将在所有正向步骤完成后才执行。

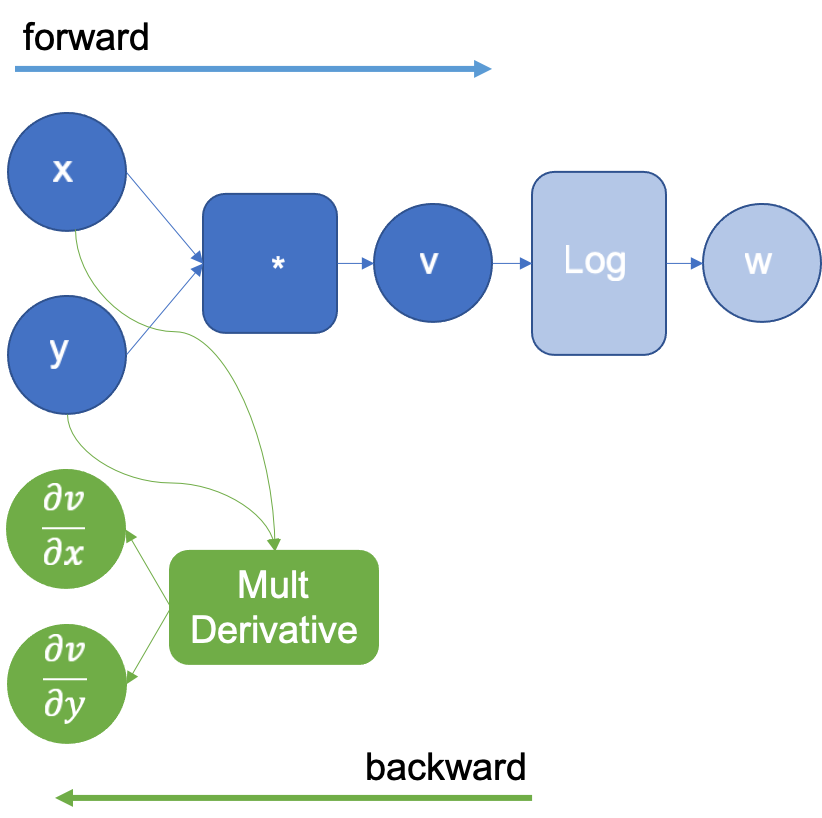
图 2：执行对数操作后扩展的计算图

继续进行，引擎现在计算 $log(v)$ 操作，并使用它所知道的 $\frac{1}{v}$ 对数导数再次扩展图。这如图 3 所示。此操作生成 $\frac{\partial w}{\partial v}$ 结果，当反向传播并乘以链式法则中的乘法导数时，生成 $\frac{\partial w}{\partial x}$ 、 $\frac{\partial w}{\partial y}$ 导数。

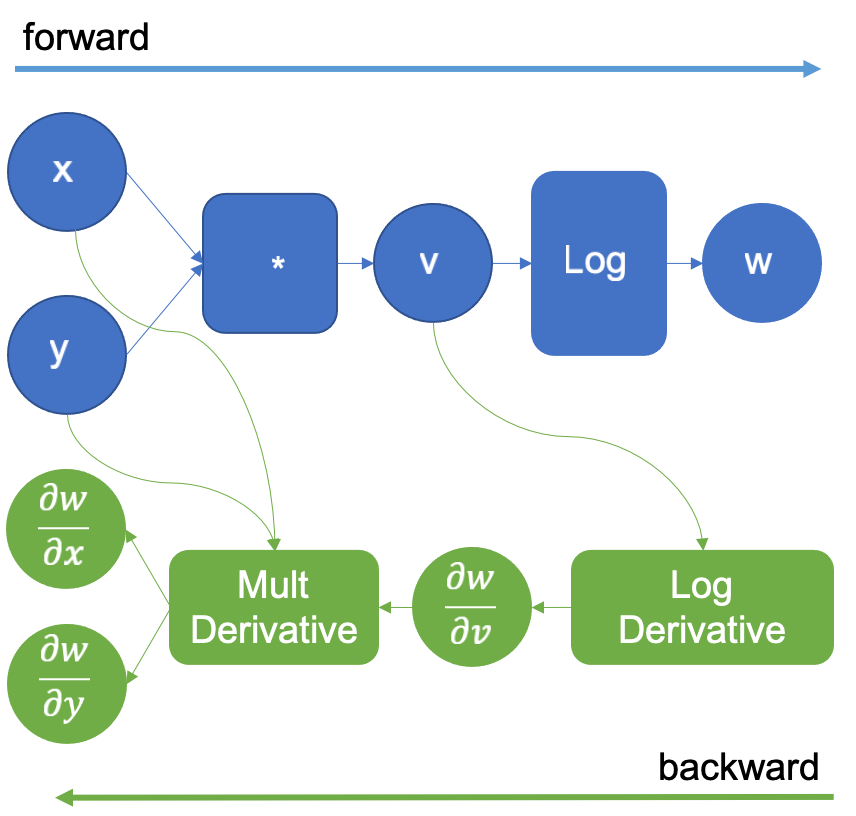
图 3：执行对数后的计算图扩展

原始计算图通过添加一个与 w 相同的新的虚拟变量 z 进行扩展。z 相对于 w 的导数是 1，因为它们是相同的变量，这个技巧允许我们应用链式法则来计算输入的导数。正向传播完成后，我们开始反向传播，为 $\frac{\partial z}{\partial w}$ 提供初始值 1.0。这如图 4 所示。

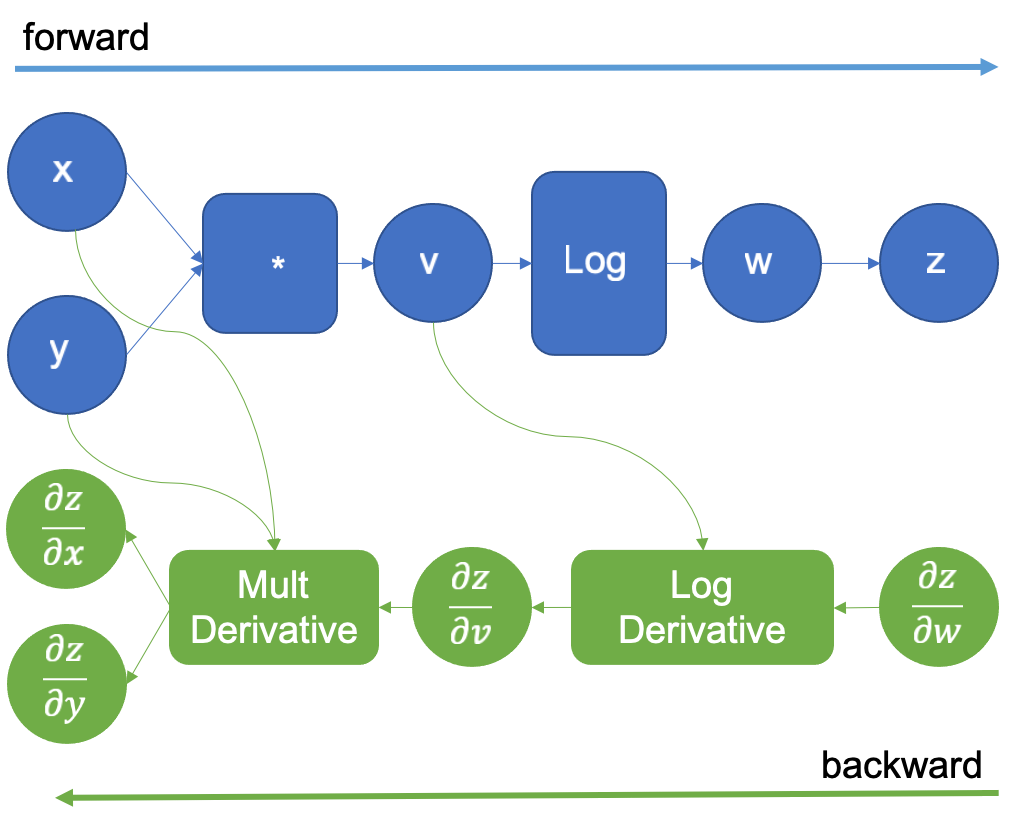
图 4：反向自动微分扩展的计算图

然后，在绿色图表之后，我们执行 LogDerivative 操作 $\frac{1}{v}$ ，这是自动微分引擎引入的，然后将结果乘以 $\frac{\partial z}{\partial w}$ ，根据链式法则获得梯度 $\frac{\partial z}{\partial v}$ 。接下来，以同样的方式执行乘法导数，最终获得所需的导数 $\frac{\partial z}{\partial x} \frac{\partial z}{\partial y}$ 。

形式上，我们在这里所做的是计算雅可比-向量积（Jvp），以计算模型参数的梯度，因为模型参数和输入都是向量。PyTorch 自动微分引擎也是如此。

雅可比-向量积

当我们计算一个向量值函数 $f(\overline{x}) = \overline{y}$ （输入和输出都是向量的函数）的梯度时，我们实际上是在构建一个雅可比矩阵。

多亏了链式法则，将函数 $f(\overline{x}) = \overline{y}$ 的雅可比矩阵与标量函数 $z = g(\overline{y})$ 的先前计算梯度相乘，可以得到关于向量值函数输入的标量输出梯度 $\frac{\partial z}{\partial x_1} \cdots \frac{\partial z}{\partial x_n}$ 。

例如，让我们用 Python 的表示法来看一些函数，以展示链式法则的应用。

$f(x_1, x_2) = (log(x_1 x_2), sin(x_2))$


def f(x1, x2):
a = x1 * x2
y1 = log(a)
y2 = sin(x2)
return (y1, y2)

$g(y_1, y_2) = y_1 y_2$


def g(y1, y2):
return y1 * y2

现在，如果我们手动通过链式法则和导数的定义来推导，我们得到以下一组可以直接代入 $f(x_1, x_2)$ 雅可比矩阵的恒等式

$\frac{\partial y_1}{\partial x_1} = \frac{\partial y_1}{\partial a}\frac{\partial a}{\partial x_1} = \frac{1}{x_1}$

$\frac{\partial y_1}{\partial x_2} = \frac{\partial y_1}{\partial a}\frac{\partial a}{\partial x_2} = \frac{1}{x_2}$

$\frac{\partial y_2}{\partial x_1} = 0$

$\frac{\partial y_2}{\partial x_2} = cos(x_2)$

接下来，让我们考虑标量函数 $z = g(y_1, y_2)$ 的梯度

$\frac{\partial z}{y_1} = y_2$

$\frac{\partial z}{y_2} = y_1$

如果我们现在计算遵循链式法则的转置-雅可比向量积，我们得到以下表达式：

$\begin{pmatrix}\frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} \\\\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} \end{pmatrix}^{t} \begin{pmatrix} y_2\\y_1 \end{pmatrix} = \begin{pmatrix}\frac{1}{x_1} & \frac{1}{x_2} \\\\ 0 & cos(x_2)) \end{pmatrix}^{t} \begin{pmatrix} y_2\\y_1 \end{pmatrix} = \begin{pmatrix} \frac{1}{x_1}y_2\\\frac{1}{x_2}y_2+cos(x_2)y_1 \end{pmatrix}$

评估 Jvp 对于 $(x_1, x_2) = (0.5, 0.75)$ 的结果为： $(\frac{dy}{x_1}, \frac{dy}{x_2}) = (1.3633, 0.1912)$ 我们可以在 PyTorch 中执行相同的表达式并计算输入的梯度：


>>> 导入 torch

>>> x = torch.tensor([0.5, 0.75], requires_grad=True)

>>> y = torch.log(x[0] * x[1]) * torch.sin(x[1])

>>> y.backward(1.0)

>>> x.grad

矩阵([1.3633, 0.1912])

结果与我们的手算雅可比-向量积相同！然而，PyTorch 从未构建矩阵，因为矩阵可能会变得过大，而是创建了一个操作图，在反向遍历的同时应用了在 tools/autograd/derivatives.yaml 中定义的雅可比-向量积。

正在遍历图

每当 PyTorch 执行一个操作时，autograd 引擎都会构建要反向遍历的图。反向模式自动微分从在末尾添加一个标量变量 $z = w$ 开始，正如我们在引言中看到的。这就是提供给 Jvp 引擎计算的初始梯度值，正如我们在上面的章节中看到的。

在 PyTorch 中，用户在调用 backward 方法时，会显式地设置初始梯度。

然后，Jvp 计算开始，但它永远不会构建矩阵。相反，当 PyTorch 记录计算图时，会添加执行的前向操作的导数（反向节点）。图 5 显示了之前看到的函数 $f(x_1, x_2)$ 和 $g(y_1, y_2)$ 的执行生成的反向图。

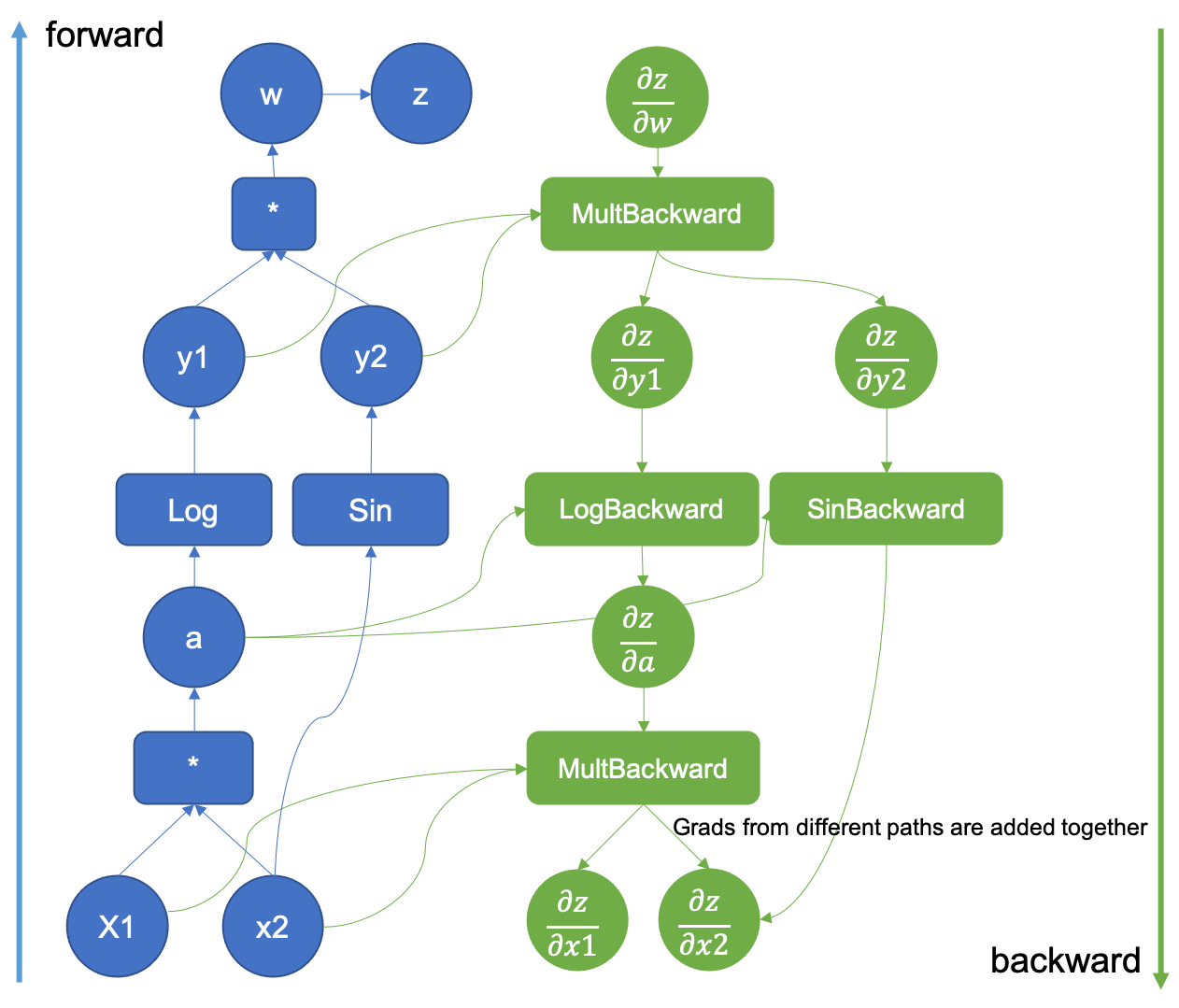
图 5：扩展反向传播的计算图

前向传播完成后，结果被用于反向传播，其中计算图中的导数被执行。基本的导数存储在 tools/autograd/derivatives.yaml 文件中，它们不是常规导数，而是它们的 Jvp 版本[3]。它们将原始函数的输入和输出以及函数输出相对于最终输出的梯度作为参数。通过反复将得到的梯度与图中下一个 Jvp 导数相乘，根据链式法则生成直到输入的梯度。

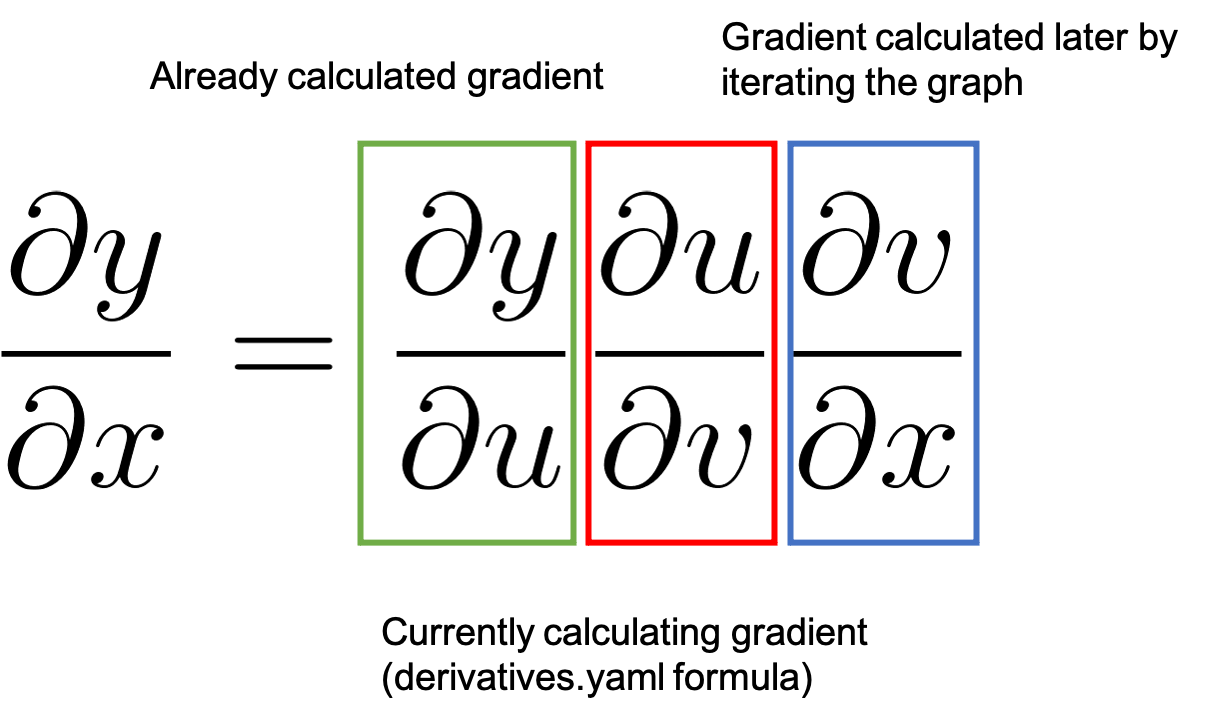
图 6：链式法则在反向微分中的应用

图 6 展示了通过链式法则的过程。我们从一个 1.0 的值开始，正如之前详细说明的那样，这是已经计算出的梯度 $\frac{\partial y}{\partial u}$ ，用绿色突出显示。然后我们移动到图中的下一个节点。在 derivatives.yaml 中注册的导数函数将计算相关的 $\frac{\partial u}{\partial v}$ 值，用红色突出显示，并将其乘以 $\frac{\partial y}{\partial u}$ 。根据链式法则，这导致 $\frac{\partial y}{\partial v}$ ，这是我们处理图中的下一个反向节点时已经计算出的梯度（绿色）。

你可能也注意到了，在图 5 中，有两个不同来源生成的梯度。当两个不同的函数共享一个输入时，对于该输入的输出梯度会被汇总，并且使用该梯度进行的计算不能进行，除非所有路径都被汇总在一起。

让我们看看在 PyTorch 中如何存储导数的一个例子。

假设我们目前正在处理 $log$ 函数的反向传播，在图 2 中的 LogBackward 节点。 $log$ 在 derivatives.yaml 中的导数被指定为 grad.div(self.conj()) 。 grad 是已经计算出的梯度 $\frac{\partial z}{\partial y1}$ ，而 self.conj() 是输入向量的复共轭。对于复数，PyTorch 计算一种特殊的导数，称为共轭 Wirtinger 导数[6]。这种导数通过[6]中描述的一些魔法操作，当将其插入优化器时，它们是下降最快的方向。

这段代码对应于图 3 中的 $(\frac{\partial z}{\partial y1} \frac{1}{v})$ ，以及相应的绿色和红色方块。继续执行，autograd 引擎将执行下一个操作；乘法的反向。和之前一样，输入是原始函数的输入以及从 $log$ 反向步骤计算出的梯度。这一步将一直重复，直到我们得到关于输入的梯度，计算将完成。只有当乘法和 sin 梯度相加后， $\frac{\partial z}{x2}$ 的梯度才完成。正如你所见，我们计算了 Jvp 的等价物，但没有构建矩阵。

在下一篇文章中，我们将深入 PyTorch 代码，看看这个图是如何构建的，以及如果你想要实验的话，相关的部分在哪里！

参考文献列表

推荐：解释了为什么反向传播要以雅可比矩阵的形式正式表达

https://cs.ubc.ca/~fwood/CS340/lectures/AD1.pdf

PyTorch Autograd 引擎概述

什么是 autograd？

参考文献列表

文档

教程

资源