由巴兹尔·霍斯默撰写

使用 3D 可视化矩阵乘法表达式、具有真实权重的注意力头等。

矩阵乘法（matmuls）是当今机器学习模型的构建块。本笔记介绍了 mm，一个用于可视化 matmuls 及其组合的工具。

矩阵乘法本质上是一种三维操作。因为 mm 使用了所有三个空间维度，所以它比通常的纸上平方习语传达的意义更清晰、更直观，尤其是对于视觉/空间思维者来说（尽管不仅限于此）。

我们还可以以几何一致的方式编写矩阵乘法，因此我们可以使用相同的规则来可视化像注意力头和 MLP 层这样的复杂结构。更高级的功能，如动画不同的矩阵乘法算法、并行分区以及加载外部数据来探索实际模型的行为，都自然地建立在这个基础上。

mm 完全交互式，在浏览器中运行，并将完整状态保存在 URL 中，因此链接是可分享的会话（本笔记中的所有截图和视频都有链接，可以打开工具中的相应可视化）。本参考指南描述了所有可用功能。

我们首先介绍可视化方法，通过可视化一些简单的矩阵乘法和表达式来建立直觉，然后深入一些更广泛的例子：

  1. 投影 - 为什么这种可视化方式更好？
  2. 暖身 - 动画 - 观看规范矩阵乘分解的实际操作
  3. 暖身 - 表达式 - 快速浏览一些基本表达式构建块
  4. 注意力头内部 - 深入探讨 GPT2 和 NanoGPT 中几个注意力头的结构、值和计算行为
  5. 并行化注意力 - 通过最近 Blockwise Parallel Transformer 论文中的示例可视化注意力头并行化
  6. 注意力层中的尺寸——当我们把整个注意力层视为一个单一结构时，MHA 和 FFA 两部分看起来是什么样的？在自回归解码过程中，这幅画面又是如何变化的？
  7. LoRA——注意力头架构扩展的视觉解释
  8. 总结——下一步计划和征求反馈

1 概述

mm 的可视化方法基于这样一个前提，即矩阵乘法本质上是一种三维操作。

换句话说就是：

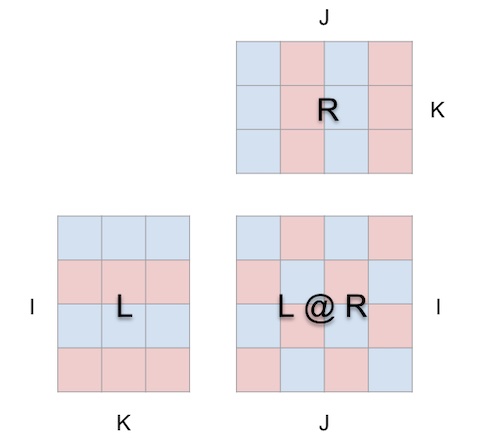
matrix multiplication is fundamentally a three-dimensional operation

是一张试图成为这样的纸（在 mm 中打开）：

wrap the matmul around a cube

当我们将 matmul 以这种方式包裹在立方体上时，参数形状、结果形状和共享维度之间的正确关系就自然地落位了。

现在的计算具有几何意义：结果矩阵中的每个位置 i, j 都锚定一个沿着立方体内部深度维度 k 运行的向量，其中从行 i 在 L 延伸的水平平面与从列 j 在 R 延伸的垂直平面相交。沿着这个向量，左、右参数中的 (i, k) (k, j) 元素成对相遇并相乘，然后将乘积沿 k 求和，并将结果存放在结果的位置 i, j 。

（暂时跳过，这里有一个动画。）

这是矩阵乘法的直观意义：

  1. 将两个正交矩阵投影到立方体的内部
  2. 将每个交点的值相乘，形成一个乘积网格
  3. 沿第三个正交维度求和以生成结果矩阵。

为了定位，该工具在立方体内部显示一个箭头，指向结果矩阵，左侧参数有一个蓝色叶片，右侧参数有一个红色叶片。工具还显示白色指南，以指示每个矩阵的行轴，尽管在这张截图上它们很淡。

布局约束很简单：

  • 左边参数和结果必须沿着它们共享的高度（i）维度拼接
  • 右边参数和结果必须沿着它们共享的宽度（j）维度拼接
  • 左边和右边参数必须沿着它们共享的（左宽度/右高度）维度拼接，这成为矩阵乘法的深度（k）维度

这种几何形状为我们可视化所有标准矩阵乘法分解提供了一个坚实的基础，并为探索非平凡复杂的矩阵乘法组合提供了一个直观的基础，正如我们下面将要看到的。

2 暖身 - 动画

在深入一些更复杂的例子之前，我们将通过几个直觉构建器来感受这种可视化风格的外观和感觉。

2a 点积

首先，标准的算法——通过计算对应左行和右列的点积来得到每个结果元素。我们在动画中看到的是乘积向量扫过立方体内部，每个向量在对应位置提供总和结果。

这里， L 有填充着 1（蓝色）或 -1（红色）的行块； R 有类似填充的列块。 k 这里是 24，所以结果矩阵（ L @ R ）的蓝色值为 24，红色值为 -24（在 mm 中打开 - 长按或按住 Ctrl 点击查看值）：

2b 矩阵-向量乘积

将 matmul 分解为矩阵-向量乘积看起来像是一个垂直平面（左参数与右参数的每一列的乘积），它在水平穿过立方体内部时将列绘制到结果中（在 mm 中打开）：

观察分解的中间值可以非常有趣，即使在简单的例子中也是如此。

例如，注意当我们使用随机初始化的参数时，中间矩阵-向量乘积中突出的垂直模式——反映了每个中间结果都是左参数的列缩放副本（在 mm 中打开）：

2c 向量-矩阵乘法

将 matmul 分解为向量-矩阵乘法看起来像一幅水平平面的绘画，将行绘制到立方体内部的结果上（在 mm 中打开）：

转换到随机初始化的参数，我们看到与矩阵-向量乘法中看到的类似模式——只是这次模式是水平的，对应于每个中间向量-矩阵乘法都是右参数的行缩放副本。

当思考矩阵乘法如何表达其参数的秩和结构时，想象这两种模式在计算中同时发生是有用的（在 mm 中打开）：

这里还有一个使用向量矩阵乘法的直觉构建器，展示了单位矩阵如何像一面 45 度角的镜子，同时映射其对立面和结果（在 mm 中打开）：

2D 求和的外积

第三种平面分解是沿着 k 轴，通过向量外积的点积求和来计算矩阵乘法的结果。在这里，我们看到外积的平面像扫过立方体“从后向前”，积累成结果（在 mm 中打开）：

使用随机初始化的矩阵进行这种分解，我们可以看到不仅值会累积在结果中，而且秩也会累积，因为每个秩-1 的外积都会被添加进去。

这在许多方面都建立了对“低秩分解”（即通过构造深度维度小的 matmul 来逼近矩阵）为什么在逼近低秩矩阵时效果最好的直觉。在下一节中介绍 LoRA（在 mm 中打开）：

3 预热 - 表达式

我们如何将这种可视化方法扩展到 matmuls 的组合？到目前为止，我们的例子都只可视化了单个矩阵乘法 L @ R 的一些矩阵 L 和 R - 当 L 和/或 R 本身也是矩阵乘法时，以及如此类推的传递性呢？

结果表明，我们可以很好地将这种方法扩展到复合表达式。关键规则很简单：子表达式（子节点）的矩阵乘法是另一个立方体，它受到与父节点相同的布局约束，并且子节点的结果面同时是父节点的对应参数面，就像共价共享的电子一样。

在这些约束下，我们可以随意安排子节点矩阵乘法的面。这里我们使用工具的默认方案，该方案生成交替的凸面和凹面立方体——这种布局在实际中效果很好，可以最大化空间利用率并最小化遮挡。（布局可以完全自定义，有关详细信息，请参阅参考资料。）

在本节中，我们将可视化机器学习模型中的一些关键构建块，以掌握视觉语言，并了解简单示例可以给我们带来哪些直觉。

3a 左结合表达式

我们将探讨两种形式的 (A @ B) @ C ，每种都有其独特的形状和特征。（注意：mm 遵循矩阵乘法左结合的惯例，并将其简单地写作 A @ B @ C 。）

首先，我们将给 A @ B @ C 赋予特征 FFN 形状，其中“隐藏维度”比“输入”或“输出”维度更宽。（具体来说，在本例的上下文中，这意味着 B 的宽度大于 A 或 C 的宽度。）

如单次 matmul 示例所示，浮动的箭头指向结果矩阵，蓝色叶片来自左侧参数，红色叶片来自右侧参数（在 mm 中打开）：

As in the single matmul examples, the floating arrows point towards the result matrix, blue vane coming from the left argument and red vane from right argument

接下来，我们将可视化 A @ B @ C ，其中 B 的宽度比 A 或 C 窄，给它一个瓶颈或“自动编码器”形状（在 mm 中打开）：

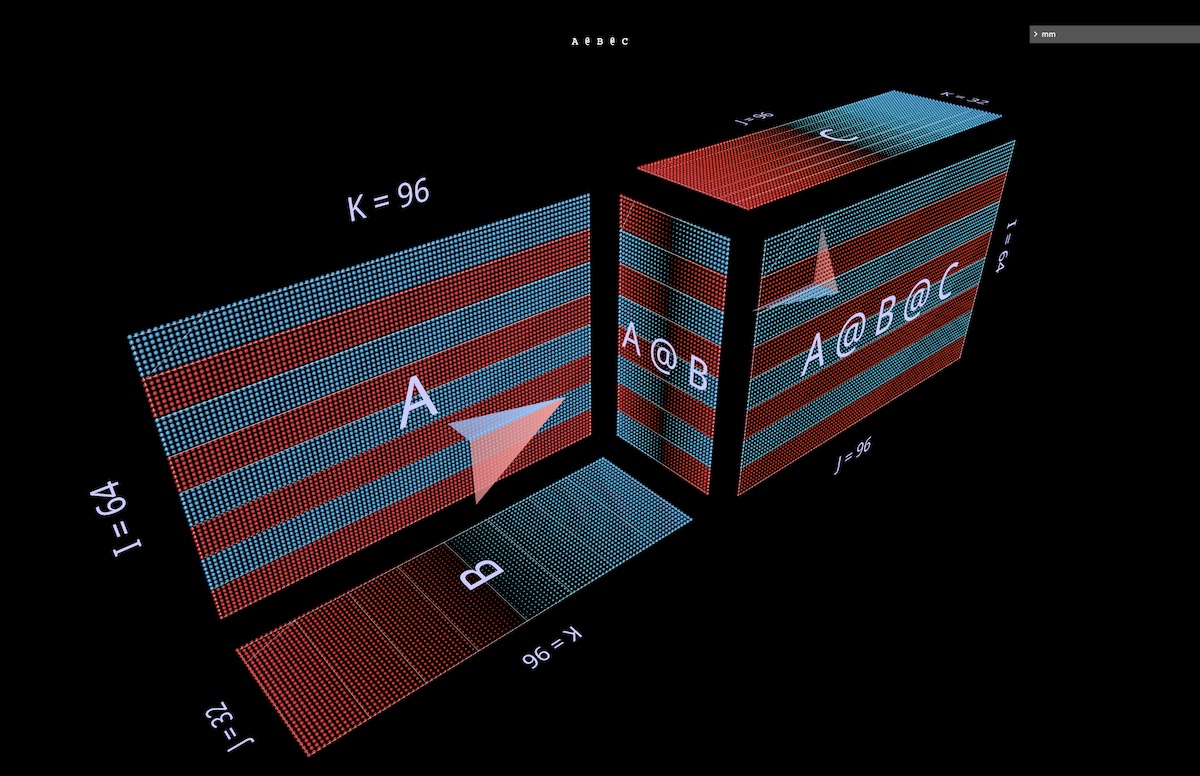
visualize A @ B @ C with the width of B narrower than that of A or C

这种交替凸凹块的模式扩展到任意长度的链：例如这个多层瓶颈（以毫米为单位打开）：

pattern of alternating convex and concave blocks extends to chains of arbitrary length

3b 右结合表达式

接下来我们将可视化一个右结合表达式 A @ (B @ C) 。

同样地，左结合表达式在水平方向上扩展——可以说是从根表达式的左参数生长出来，因此右结合链在垂直方向上扩展，从根的右参数生长出来。

有时可以看到一个多层感知器（MLP）被正确地表示，即输入列在右侧，权重层从右向左运行。使用上面图片中 2 层前馈神经网络（FFN）示例中的矩阵——适当转置——这就是它的样子，其中 C 现在扮演输入的角色， B 是第一层， A 是第二层（在 mm 中打开）：

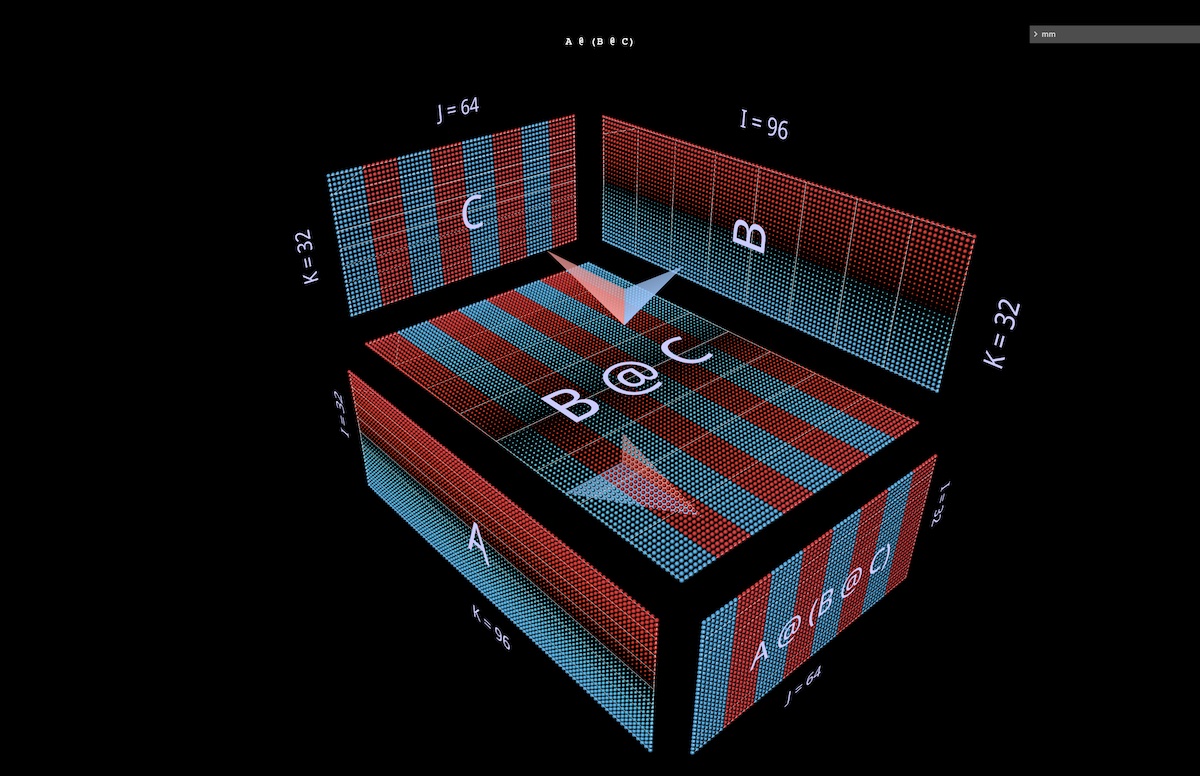
an MLP formulated right-associatively

顺便说一句，除了箭头叶片的颜色（左侧为蓝色，右侧为红色）外，区分左右参数的第二个视觉线索是它们的朝向：左侧参数的行与结果的行共面——它们沿着同一轴堆叠（ i ）。这两个线索都告诉我们，例如， B 是上面 (B @ C) 的左侧参数。

3c 二元表达式

对于一个可视化工具要超越简单的教学示例而变得有用，随着表达式变得更加复杂，可视化需要保持可读性。在现实世界的用例中，一个关键的结构组件是二元表达式——具有左右两侧子表达式的矩阵乘法。

我们将可视化这种最简单的表达式形状， (A @ B) @ (C @ D) （在毫米中打开）：

binary expressions - matmuls with subexpressions on both the left and right

3d 快速旁白：分区和并行性

尽管这个主题的完整介绍超出了本笔记的范围，但我们将稍后在注意力头部的上下文中看到它的实际应用。但作为热身，两个快速示例应该能让人感受到这种风格的可视化如何使关于并行化复合表达式的推理变得非常直观，通过简单的分区几何来实现。

在第一个例子中，我们将对上述左结合的多层瓶颈示例应用经典的“数据并行”分区。我们沿着 i 进行分区，将初始左参数（“批次”）和所有中间结果（“激活”）进行分段，但后续参数（“权重”）除外——这种几何结构使得很明显哪些表达式参与者被分割，哪些保持完整（在毫米中打开）：

the canonical "data parallel" partitioning to the left-associative multilayer bottleneck example

第二个例子（对我来说）可能更难建立直觉，因为没有清晰的几何图形来支持它：它展示了如何通过沿其 j 轴对左子表达式进行分区、沿其 i 轴对右子表达式进行分区以及沿其 k 轴对父表达式进行分区来并行化二进制表达式（在毫米中打开）：

a binary expression can be parallelized by partitioning the left subexpression along its j axis, the right subexpression along its i axis, and the parent expression along its k axis

4 在注意力头内部

让我们看看一个 GPT2 注意力头——具体来说是“gpt2”（小型）配置（层数=12，头数=12，嵌入=768）的第 5 层第 4 个头，使用 OpenAI 权重通过 HuggingFace。输入激活是从对 OpenWebText 训练样本的 256 个标记的前向传递中获取的。

这个特定的头没有什么特别不寻常的地方；我主要选择它是因为它计算了一个相当常见的注意力模式，并且位于模型的中间，那里的激活已经变得结构化并显示出一些有趣的纹理。（顺便说一句：在随后的笔记中，我将展示一个注意力头探索器，它允许您可视化此模型的全部层和头，以及一些旅行笔记。）

在 mm 中打开（获取模型权重可能需要几秒钟）

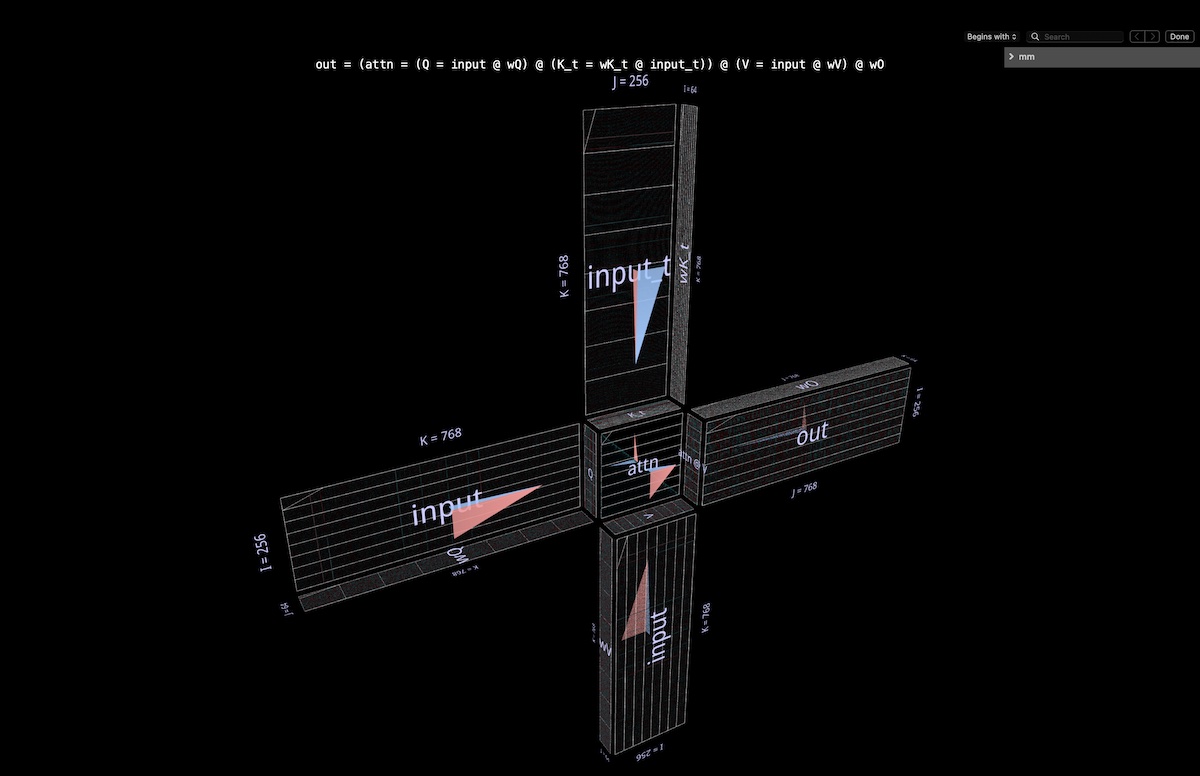
There's nothing particularly unusual about this particular head

4a 结构

整个注意力头被可视化为一个单一复合表达式，从输入开始到投影输出结束。（注意：为了保持内容的完整性，我们按照 Megatron-LM 中描述的方法进行每头输出投影。）

计算包含六个矩阵乘法：

Q = input @ wQ        // 1
K_t = wK_t @ input_t  // 2
V = input @ wV        // 3
attn = sdpa(Q @ K_t)  // 4
head_out = attn @ V   // 5
out = head_out @ wO   // 6

我们正在查看的缩略图描述：

  • 风车叶片的乘积为 1、2、3 和 6：前者是输入到 Q、K 和 V 的内部投影；后者是从 attn @ V 到嵌入维度的输出投影。
  • 在中心轴处是双重矩阵乘法，首先计算注意力分数（后面的凸立方体），然后使用它们从值向量中生成输出标记（前面的凹立方体）。因果性意味着注意力分数形成一个下三角。

但我鼓励您在工具本身中探索这个示例，而不是依赖下面的截图或视频来传达从中可以吸收多少信号——关于其结构和实际计算中流动的实际值。

4b 计算与值

这里是一个注意力头计算的动画。具体来说，我们正在观察

sdpa(input @ wQ @ K_t) @ V @ wO

（即上面提到的矩阵乘法 1、4、5 和 6，其中 K_t 和 V 已预计算）作为一个融合的向量-矩阵乘积链被计算：序列中的每个项目都一步从输入通过注意力到输出。关于这个动画选择，在后续关于并行化的章节中会有更多介绍，但首先让我们看看正在计算的价值告诉我们什么。

在 mm 中打开

这里正在进行许多有趣的事情。

  • 在我们进行注意力计算之前， Q 和 K_t 的低秩就已经相当引人注目。在放大 Q @ K_t 向量-矩阵乘法动画时，情况更加明显： Q 和 K 中的许多通道（嵌入位置）在整个序列中几乎保持不变，这意味着有用的注意力信号可能只由嵌入的小部分驱动。理解和利用这一现象是我们作为 SysML ATOM 变换器效率项目的一部分正在拉动的线索之一。
  • 最熟悉的是注意力矩阵中出现的强大但并不完美的对角线。这是一个常见的模式，出现在这个模型（以及许多变换器）的许多注意力头中。它产生局部化的注意力：输出位置前的小邻域中的值标记在很大程度上决定了输出标记的内容模式。
  • 然而，这个邻域的大小以及其中各个标记的影响程度差异很大——这可以从注意力网格的偏对角线霜冻以及 attn[i] @ V 向量-矩阵乘积平面上随注意力矩阵在序列中下降时波动的模式中看出。
  • 但请注意，吸引注意力的不仅仅是局部邻域：注意力网格的最左侧列，对应于序列的第一个标记，完全由非零（但波动）的值填充，这意味着每个输出标记都会在一定程度上受到第一个标记值的影响。
  • 此外，当前标记邻域与初始标记之间的注意力分数主导权存在不精确但可辨别的振荡。振荡的周期各不相同，但总的来说，随着向下移动序列，周期开始较短，然后变长（与每行的候选注意力标记数量相关，考虑到因果关系）。
  • 要了解（ attn @ V) ）是如何形成的，重要的是不要孤立地关注注意力 - V 同样是一个重要的角色。每个输出项是整个 V 向量的加权平均值：在注意力完美对角化的极限情况下， attn @ V 简单地是 V 的精确副本。在这里我们看到的是更丰富的景象：可见的条纹，其中某些标记在连续的注意力行子序列中得分很高，叠加在一个与 V 相似但垂直方向上有些模糊的矩阵上。（旁白：根据 mm 参考指南，长按或控制点击将显示可视化元素的数值。）
  • 请记住，由于我们处于中间层（5），这个注意力头的输入是一个中间表示，而不是原始的标记化文本。因此，输入中看到的模式本身就很有启发性 - 特别是，强烈的垂直纹理是那些在整个序列中值均匀且幅度很高的特定嵌入位置 - 有时几乎涵盖了整个序列。
  • 有趣的是，输入序列中的第一个向量非常独特，不仅打破了这些高幅度列的规律，而且在几乎每个位置都携带了非典型值（顺便说一句：这里没有可视化，但这种模式在多个样本输入中重复出现）。

注意：关于最后两个要点，值得重申的是，我们正在可视化单个样本输入的计算。在实践中，我发现每个头都会在相当数量的样本中持续表达其特有的模式（尽管不是完全相同），即将推出的注意力头浏览器将提供一组样本以供玩耍，但在查看包含激活的任何可视化时，重要的是要记住，输入的全部分布可能会以微妙的方式影响它所激发的想法和直觉。

最后，再提一次，直接探索动画吧！

4c 头部以有趣的方式不同

在我们继续之前，这里还有一个简单的演示，展示了简单地探索模型以了解其工作细节的有用性。

这是 GPT2 的另一个注意力头。它与第 5 层第 4 个头的行为相当不同——正如人们所预期的，因为它位于模型的非常不同的部分。这个头在第一层：第 0 层，第 2 个头（在 mm 中打开，可能需要几秒钟来加载模型权重）：

This is another attention head from GPT2

注意事项：

  • 这个头将注意力非常均匀地分散。这导致对 V （或者更确切地说， V 的适当因果前缀）中的每一行提供一个相对未加权的平均值，如动画所示：当我们向下移动注意力分数三角形时， attn[i] @ V 向量-矩阵乘积与简单地缩小、逐渐揭示的 V 的微小波动。
  • attn @ V 具有显著的垂直一致性 - 在嵌入的大型柱状区域中，相同的值模式在整个序列中持续存在。可以将其视为每个标记共享的属性。
  • 顺便说一句，一方面，鉴于非常均匀分布的注意力效应，人们可能会期望 attn @ V 中存在一些一致性。但每一行都只由 V 的因果子序列构建而成，而不是整个序列 - 为什么这不会导致更多的变化，就像随着序列向下移动而逐渐变形一样？通过视觉检查，V 在其长度上并不均匀，因此答案必须在于其值分布的某些更微妙的属性。
  • 最后，这个头部的输出在投影后甚至更加垂直一致。
  • 给人的强烈印象是，这个注意力头部传递的大部分信息都是由序列中每个标记共享的属性组成的。其输出投影权重的组成加强了这一直觉。

总体来说，很难抗拒这样一个想法：这个注意力头产生的极其规律、高度结构化的信息可能是由一些稍微……不那么奢侈的计算手段获得的。当然，这并不是一个未开发的领域，但可视化计算信号的特定性和丰富性在产生新想法和推理现有想法方面已经很有用。

4d 重访音高：免费的不变量

退一步，值得重申的是，我们之所以能够可视化非平凡的复合操作，如注意力头，并且使它们保持直观，是因为重要的代数属性——比如论证形状是如何被约束的，或者哪些并行化轴与哪些操作相交——不需要额外的思考：它们直接来自可视化对象的几何形状，而不是额外的规则需要记住。

例如，在这些注意力头可视化中，立即就可以明显看出

  • Q 和 attn @ V 长度相同， K 和 V 长度相同，且这些对的长度彼此独立
  • Q 和 K 宽度相同， V 和 attn @ V 宽度相同，且这些对的宽度彼此独立。

这些属性通过构造是真实的，这是由于化合物结构中组成部分所在的位置以及它们的取向的简单结果。

这种“免费属性”的好处，在探索规范结构的变体时特别有用——一个明显的例子是在自回归逐个标记解码中一行的注意力矩阵（在 mm 中打开）：

the one-row-high attention matrix in autoregressive token-at-a-time decoding

5 并行化注意力

在动画中，头部 5 的第四层，我们可视化了注意力头部中的 6 个 matmuls 中的 4 个

作为一个融合的向量-矩阵乘积链，证实了整个从输入到输出的左结合链沿着共享的 i 轴是层状的，并且可以并行化。

5a 示例：沿 i 分区

在实践中，为了并行计算，我们会将输入沿 i 轴划分为多个块。我们可以在工具中通过指定某个轴被划分为特定数量的块来可视化这种划分 - 在这些示例中我们将使用 8，但这个数字并没有什么特殊的意义。

此外，这种可视化清楚地表明，对于投影（in-projection）的 wQ 、注意（attention）的 K_t 和 V 以及输出投影（out-projection）的 wO ，每个并行计算都需要它们的全部，因为它们与那些矩阵沿未划分维度相邻（在 mm 中打开）。

wQ (for in-projection), K_t and V (for attention) and wO (for out-projection) are needed in their entirety by each parallel computation

5b 示例：双重划分

作为沿多个轴划分的示例，我们可以可视化一些在这个领域创新的研究成果（块并行变换器，基于例如 Flash Attention 及其前身的工作）。

首先，BPT 沿着 i 进行分区，如上所述——并且实际上将这种序列的水平分区扩展到了注意力层的第二（FFN）半部分。（我们将在后面的章节中可视化这一点。）

为了全面解决上下文长度问题，随后在 MHA 中添加了第二个分区——即注意力计算本身的分区（即在 Q @ K_t 的 j 轴上的分区）。这两个分区将注意力分割成网格状的块（在 mm 中打开）：

The two partitions together divide attention into a grid of blocks

这种可视化清楚地表明

  • 这种双重分区作为解决上下文长度问题的攻击方法的有效性，因为我们现在已经明显地将注意力计算中序列长度的每个出现进行了分区
  • 这个第二个分区“范围”：从几何上可以看出， K 和 V 的投影计算可以与核心双矩阵乘法一起分区

注意一个细节：这里的视觉含义是，我们还可以并行化随后的 attn @ V 矩阵乘法，并按 split-k 风格累加部分结果，从而并行化整个双矩阵乘法。但是， sdpa() 中的行向 softmax 添加了每个行必须在其对应的 attn @ V 行计算之前进行归一化的要求，在注意力计算和最终矩阵乘法之间增加了额外的行向步骤。

注意力层中的 6 个大小

注意力层的前半部分（MHA）因其二次复杂度而闻名，计算量很大，但后半部分（FFN）由于其隐藏维度的宽度（通常是模型嵌入维度的 4 倍）也很有需求。可视化整个注意力层的生物量有助于建立对层两半之间比较的直觉。

展示完整层的可视化

下面是一个完整的注意力层，前半部分（MHA）在背景中，后半部分（FFN）在前景中。通常，箭头指向计算的方向。

备注：

  • 这种可视化并没有描绘单个注意力头，而是显示了围绕中心双矩阵乘法的未切片 Q/K/V 权重和投影。当然，这并不是对完整 MHA 操作的忠实可视化——但这里的目的是更清晰地展示层两半的相对矩阵大小，而不是每半部分执行的相对计算量。（此外，使用的是随机值而不是真实权重。）
  • 这里使用的维度已缩小以保持浏览器（相对）满意，但比例得到了保留（来自 NanoGPT 的小型配置）：模型嵌入维度 = 192（从 768），FFN 嵌入维度 = 768（从 3072），序列长度 = 256（从 1024），尽管序列长度对模型并非基本。从视觉上看，序列长度的变化会表现为输入刀片的宽度变化，进而影响注意力中心的大小和下游垂直平面的高度。

以毫米为单位打开：

a full attention layer with the first half (MHA) in the background and the second (FFN) in the foreground

可视化 BPT 分区层

简要回顾块状并行转换器，在此我们可视化整个注意力层（如上所述省略了单个头）的 BPT 并行化方案。特别是注意，沿着序列块（ i ）的分区如何贯穿 MHA 和 FFN 的两半（以毫米为单位打开）。

visualize BPT's parallelization scheme in the context of an entire attention layer

6c 分割 FFN

可视化表明需要额外的分割，与上述分割正交 - 在 FFN 的注意力层一半，首先沿着 j 分割 attn_out @ FFN_1 ，然后在随后的与 FFN_2 的矩阵乘法中沿着 k 分割。这种分割切开了 FFN 权重的两层，以降低每个参与计算的参与者容量需求为代价，最终需要对部分结果进行求和。

下面是这种分割应用于一个未分割的注意力层的样子（在 mm 中打开）：

what this partition looks like applied to an otherwise unpartitioned attention layer

下面是应用于类似于 BPT 分割的层的样子（在 mm 中打开）：

applied to a layer partitioned a la BPT

逐个 token 可视化解码

在自回归逐个 token 解码过程中，查询向量由单个 token 组成。在这种情况下，想象一下注意力层的样子很有教育意义——一个嵌入行正在通过一个巨大的镶嵌权重平面。

除了强调权重相对于激活的巨大差异之外，这种视图还让人联想到 K_t 和 V 在 6 层 MLP 中像动态生成的层一样工作，尽管 MHA 本身的 mux/demux 计算（如上所述）使得这种对应并不精确（在 mm 中打开）：

the mux/demux computations of MHA itself

7 LoRA

最近关于 LoRA 的论文（LoRA：大型语言模型的低秩自适应）描述了一种基于权重变化在微调过程中是低秩这一想法的高效微调技术。根据论文，这“允许我们通过优化适应过程中密集层的权重变化矩阵的秩分解矩阵，间接地训练神经网络中的某些密集层，同时保持预训练权重冻结。”

7a 基本思想

简而言之，关键步骤是训练权重矩阵的因子而不是矩阵本身：用一个 I x K 张量和一个 K x J 张量的矩阵乘法来替换一个 I x J 权重张量，将 K 保持在一个较小的数字。

如果 K 足够小，那么尺寸优势可以非常大，但代价是降低秩会降低乘积可以表达的结构。为了快速说明尺寸节省和结构效应对结果的影响，这里是一个随机 128 x 4 左和 4 x 128 右参数的矩阵乘法 - 即一个 128 x 128 矩阵的秩-4 分解。注意 L @ R 中的垂直和水平图案（在 mm 中打开）。

a matmul of random 128 x 4 left and 4 x 128 right arguments

将 LoRA 应用于注意力头

LoRA 将这一分解操作应用于微调过程的方式是

  • 为每个需要微调的权重张量创建一个低秩分解，并训练这些因子，同时保持原始权重冻结
  • 微调完成后，将每对低秩因子相乘，得到一个与原始权重张量形状相同的矩阵，并将其添加到原始预训练权重张量中

以下可视化显示了注意力头，其中权重张量 wQ 、 wK_t 、 wV 、 wO 被低秩分解 wQ_A @ wQ_B 等所替代。从视觉上看，因子矩阵在风车叶片的边缘显示为低栅栏（在毫米空间中打开 - 空格键停止旋转）：

8 总结

8a 征求反馈

我发现这种可视化矩阵乘法表达式的做法对于建立直觉和推理非常有帮助，不仅限于矩阵乘法本身，还包括许多机器学习模型及其计算的各个方面，从效率到可解释性。

如果您尝试使用并有所建议或评论，我肯定想听听，无论是这里的评论还是仓库中的评论。

下一步 8b

  • 如上所述，将这些可视化嵌入到 Python 笔记本中非常简单。但会话 URL 可能会变得难以管理，因此拥有从配置对象构建它们的 Python 端实用程序将很有用，类似于参考指南中使用的简单 JavaScript 辅助工具。一旦完成，我计划发布一个包含清单的笔记。
  • 如上所述，将这些可视化嵌入到 Python 笔记本中非常简单。但是会话 URL 可能会变得难以管理，因此拥有从配置对象构建它们的 Python 端实用程序将很有用，类似于参考指南中使用的简单 JavaScript 辅助工具。
  • 如果您有一个可能从这种可视化中受益的场景，但不知道如何使用工具来实现，请联系我们！我并不一定想大幅扩展其核心可视化功能（适合的工具，等等），但例如，用于驱动它的 API 非常基础，那里还有很多可以做的事情。