在过去一年中,我们已将半结构化(2:4)稀疏性支持添加到 PyTorch 中。仅用几行代码,我们就能够通过用稀疏矩阵乘法替换密集矩阵乘法,在 segment-anything 上实现 10%的端到端推理速度提升。
然而,矩阵乘法并不仅限于神经网络推理,它们在训练过程中也会发生。通过扩展我们之前用于加速推理的核心原语,我们还能够加速模型训练。我们编写了一个替换 nn.Linear 层, SemiSparseLinear ,它能够在 ViT-L 的 MLP 块的前向和反向传递中实现 1.3 倍的速度提升。
在端到端的情况下,我们观察到 DINOv2 ViT-L 训练的墙时减少了 6%,并且几乎没有准确性下降(ImageNet top-1 准确率从 82.8 下降到 82.7)。
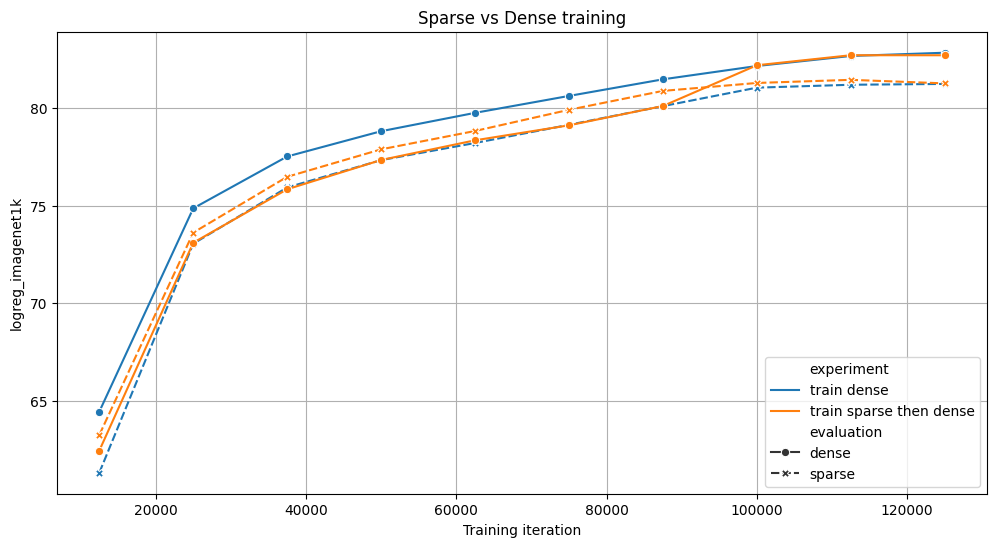
我们比较了两种在 4x NVIDIA A100s 上训练 ViT 模型 125k 次迭代的策略:一种是全连接(蓝色),另一种是 70%的训练使用稀疏,然后使用全连接(橙色)。两种方法在基准测试中取得了相似的结果,但稀疏版本的训练速度提高了 6%。对于这两个实验,我们评估了带稀疏和不带稀疏的中间检查点。
据我们所知,这是第一个加速稀疏训练的开源软件实现,我们很高兴在 torchao 中提供用户 API。您只需几行代码就可以尝试加速自己的训练运行:
# Requires torchao and pytorch nightlies and CUDA compute capability 8.0+
import torch
from torchao.sparsity.training import (
SemiSparseLinear,
swap_linear_with_semi_sparse_linear,
)
model = torch.nn.Sequential(torch.nn.Linear(1024, 4096)).cuda().half()
# Specify the fully-qualified-name of the nn.Linear modules you want to swap
sparse_config = {
"seq.0": SemiSparseLinear
}
# Swap nn.Linear with SemiSparseLinear, you can run your normal training loop after this step
swap_linear_with_semi_sparse_linear(model, sparse_config)
这是如何工作的?
稀疏性的基本思想很简单:跳过涉及零值张量元素的运算以加快矩阵乘法。然而,仅仅将权重设置为零是不够的,因为密集张量仍然包含这些剪枝元素,密集矩阵乘法内核将继续处理它们,产生相同的延迟和内存开销。为了实现真正的性能提升,我们需要用智能跳过剪枝元素的稀疏内核来替换密集内核。
这些核适用于稀疏矩阵,它们删除修剪的元素并以压缩格式存储指定的元素。稀疏格式有很多种,但我们特别关注半结构化稀疏性,也称为 2:4 结构化稀疏性或细粒度结构化稀疏性,更一般地称为 N:M 结构化稀疏性。
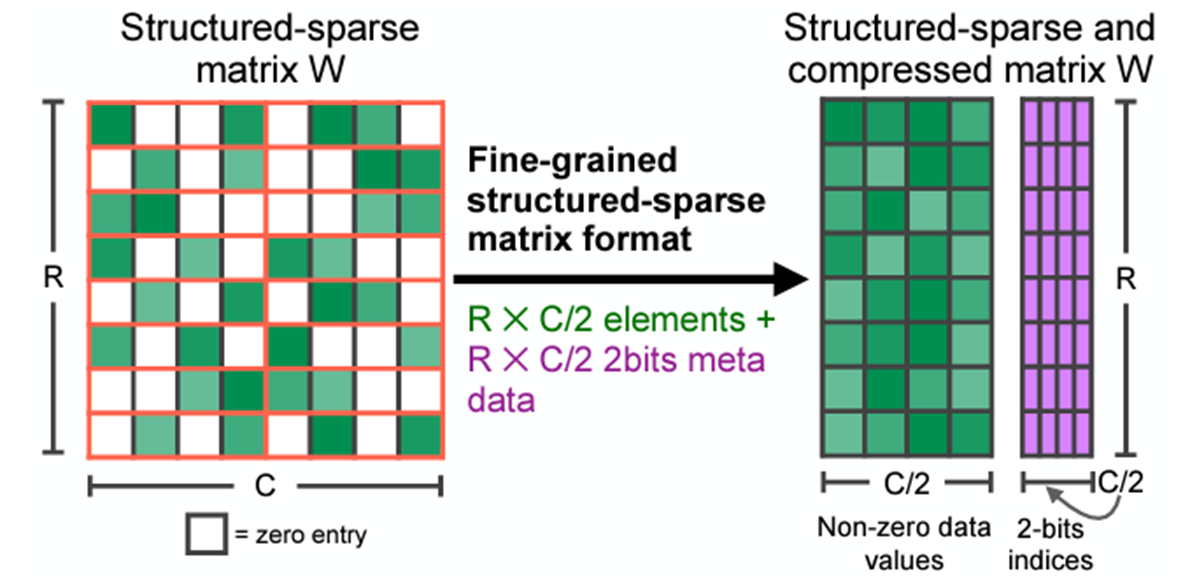
2:4 稀疏压缩表示。原始来源
2:4 稀疏矩阵是一种矩阵,其中每 4 个元素中最多只有 2 个非零元素,如上图所示。半结构化稀疏性吸引人之处在于它存在于性能和准确性的黄金分割点:
- 自 Ampere 以来,NVIDIA GPU 提供硬件加速和库支持(cuSPARSELt)为此格式,矩阵乘法速度可提高至 1.6 倍
- 对模型进行剪枝以适应这种稀疏模式并不会像其他模式那样降低精度。NVIDIA 的白皮书显示,剪枝后重新训练能够恢复大多数视觉模型的精度。

2:4(稀疏)矩阵乘法在 NVIDIA GPU 上的示意图。原始来源
使用半结构化稀疏性加速推理非常简单。由于我们的权重在推理过程中是固定的,我们可以在推理之前(离线)剪枝和压缩权重,并存储压缩后的稀疏表示,而不是我们的密集张量。
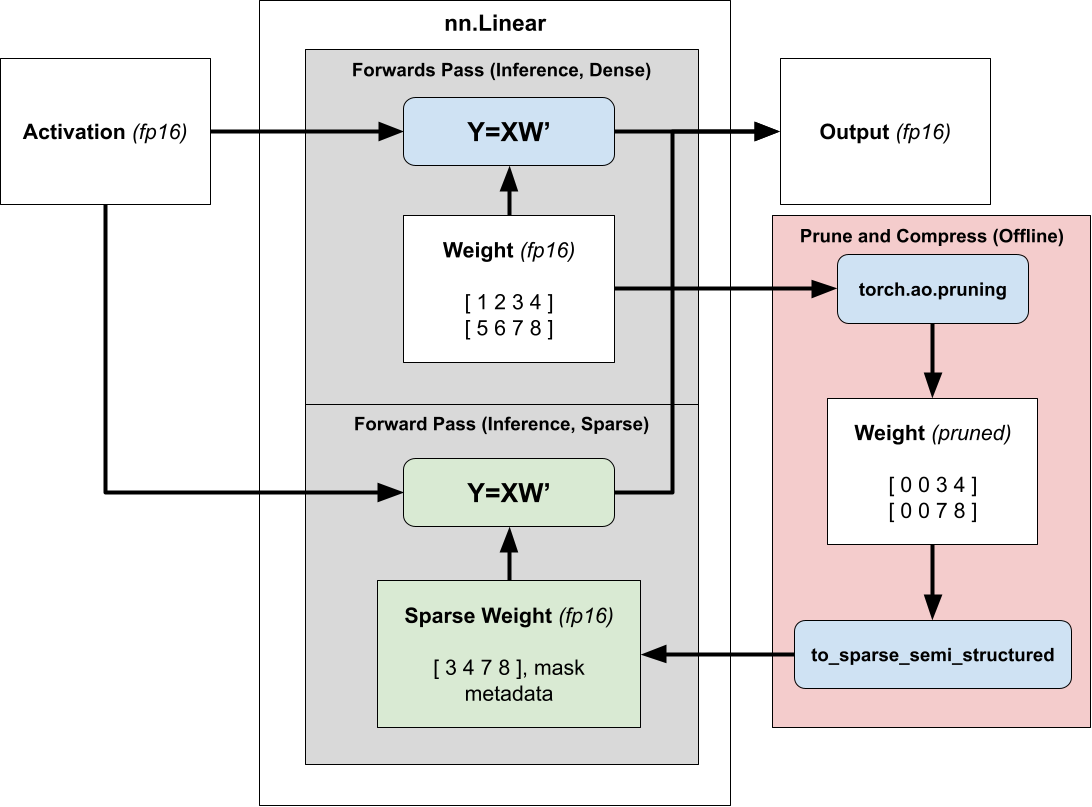
然后,我们不是调度到密集矩阵乘法,而是调度到稀疏矩阵乘法,传递压缩后的稀疏权重而不是正常的密集权重。有关使用 2:4 稀疏性加速模型推理的更多信息,请参阅我们的教程。
将稀疏推理加速扩展到训练
为了利用稀疏性来减少我们模型的训练时间,我们需要考虑何时计算掩码,因为一旦我们存储了压缩表示,掩码就固定了。
将固定掩码应用于现有已训练的密集模型(也称为剪枝)不会降低精度,但这需要两次训练运行——一次获得密集模型,另一次将其转换为稀疏,无法提供加速。
相反,我们希望从头开始训练一个稀疏模型(动态稀疏训练),但使用固定掩码从头开始训练会导致评估显著下降,因为稀疏掩码将在初始化时被选择,此时模型权重基本上是随机的。
为了在从头开始训练时保持模型的准确性,我们在运行时剪枝和压缩权重,以便在每个训练步骤中计算最优掩码。
从概念上讲,可以将我们的方法视为一种近似矩阵乘法技术,我们可以在比 `dense_GEMM` 调用少的时间内将 `prune_and_compress` 调度到 `sparse_GEMM` 。这很困难,因为本地的剪枝和压缩函数太慢,无法显示出速度提升。
考虑到我们的 ViT-L 训练矩阵乘法的形状(13008x4096x1024),我们分别测量了密集和稀疏 GEMM 的运行时间为 538us 和 387us。换句话说,权重矩阵的剪枝和压缩步骤必须在 538-387=151us 内运行,才能获得任何效率提升。不幸的是,cuSPARSELt 中提供的压缩内核已经花费了 380us(甚至没有考虑剪枝步骤!)。
考虑到最大 NVIDIA A100 内存 IO(2TB/s),并且考虑到剪枝和压缩内核可能会受到内存限制,我们理论上可以在 4 微秒内剪枝和压缩我们的权重(4096x1024x2 字节=8MB)!实际上,我们能够编写一个内核,将矩阵剪枝并压缩成 2:4 稀疏格式,运行时间为 36 微秒(比 cuSPARSELt 中的压缩内核快 10 倍),使整个 GEMM(包括稀疏化)更快。我们的内核可用于 PyTorch。
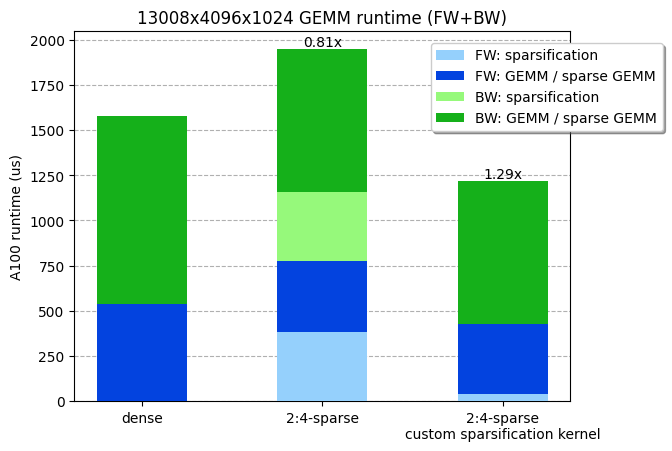
我们定制的剪枝+压缩稀疏化内核,在线性层前向+反向操作中大约快 30%。在 NVIDIA A100-80GB GPU 上进行了基准测试。
编写高性能运行时稀疏化内核
为了实现高性能的运行时稀疏化内核,我们面临了多个挑战,以下将进行探讨。
1) 处理反向传播
对于反向传播,我们需要计算 dL/dX 和 dL/dW 以进行梯度更新和后续层的计算,这意味着我们需要分别计算 xW T 和 x T W。
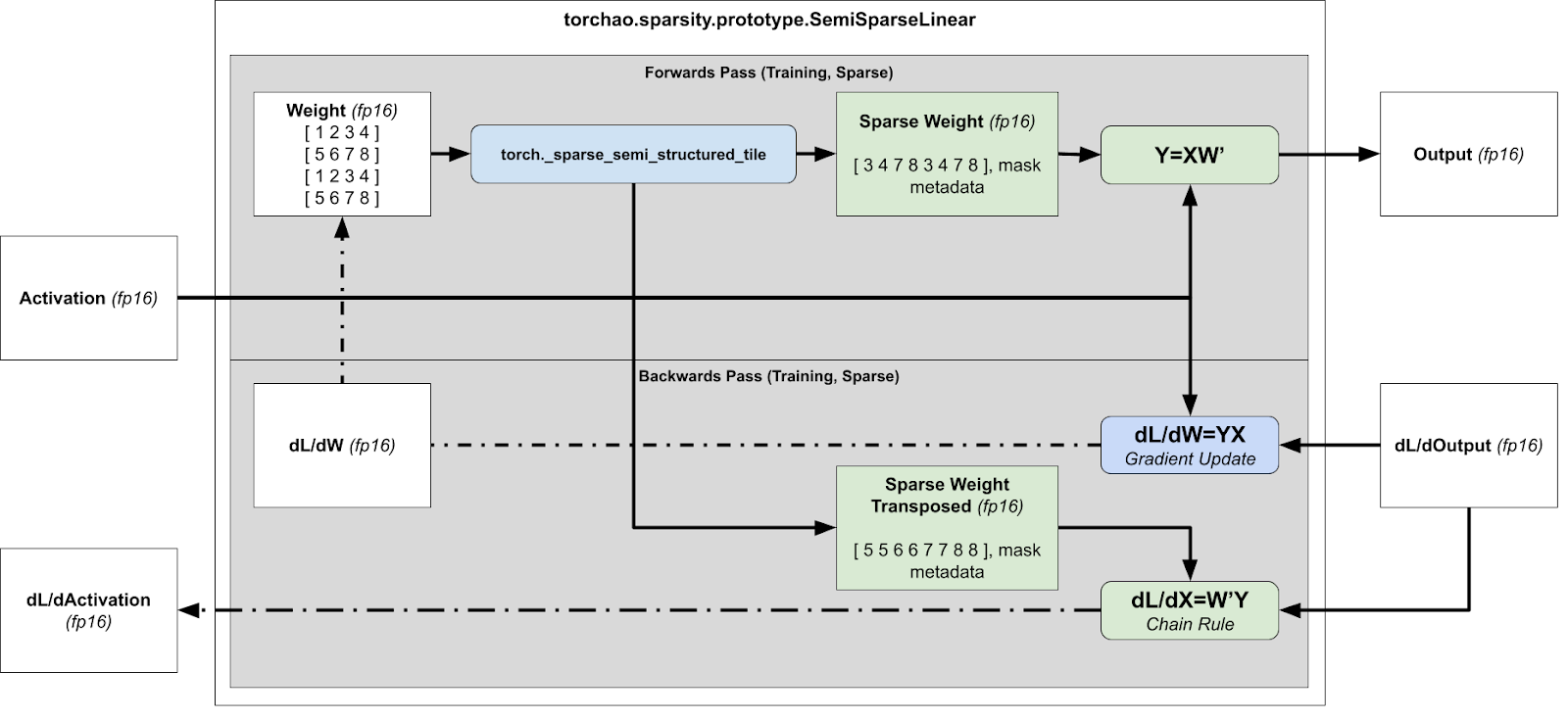
运行时稀疏化概述以加速训练(前向和反向传播)
然而,这存在问题,因为压缩表示不能转置,因为没有保证张量在两个方向上都是 2:4 稀疏的。
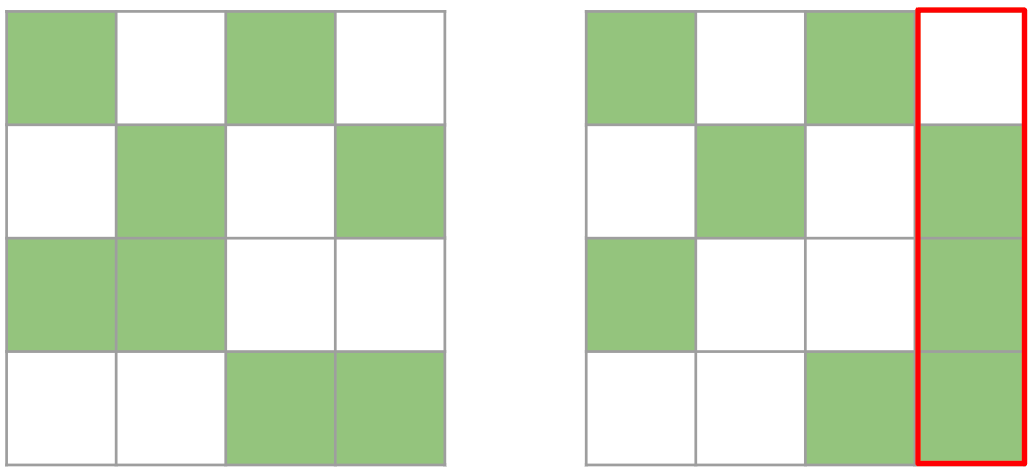
两个矩阵都是有效的 2:4 矩阵。然而,右边的矩阵一旦转置就不再是有效的 2:4 矩阵,因为其中一列包含超过 2 个元素
因此,我们剪枝一个 4x4 的瓦片,而不是 1x4 的条带。我们贪婪地保留最大的值,确保每行/每列最多只取 2 个值。虽然这种方法并不保证最优,因为我们有时只保留 7 个值而不是 8 个,但它可以有效地计算出一个行和列都是 2:4 稀疏的张量。
然后,我们同时压缩打包的张量和打包转置的张量,存储转置张量以供反向传播使用。通过同时计算打包和打包转置的张量,我们避免了反向传播中的第二次内核调用。
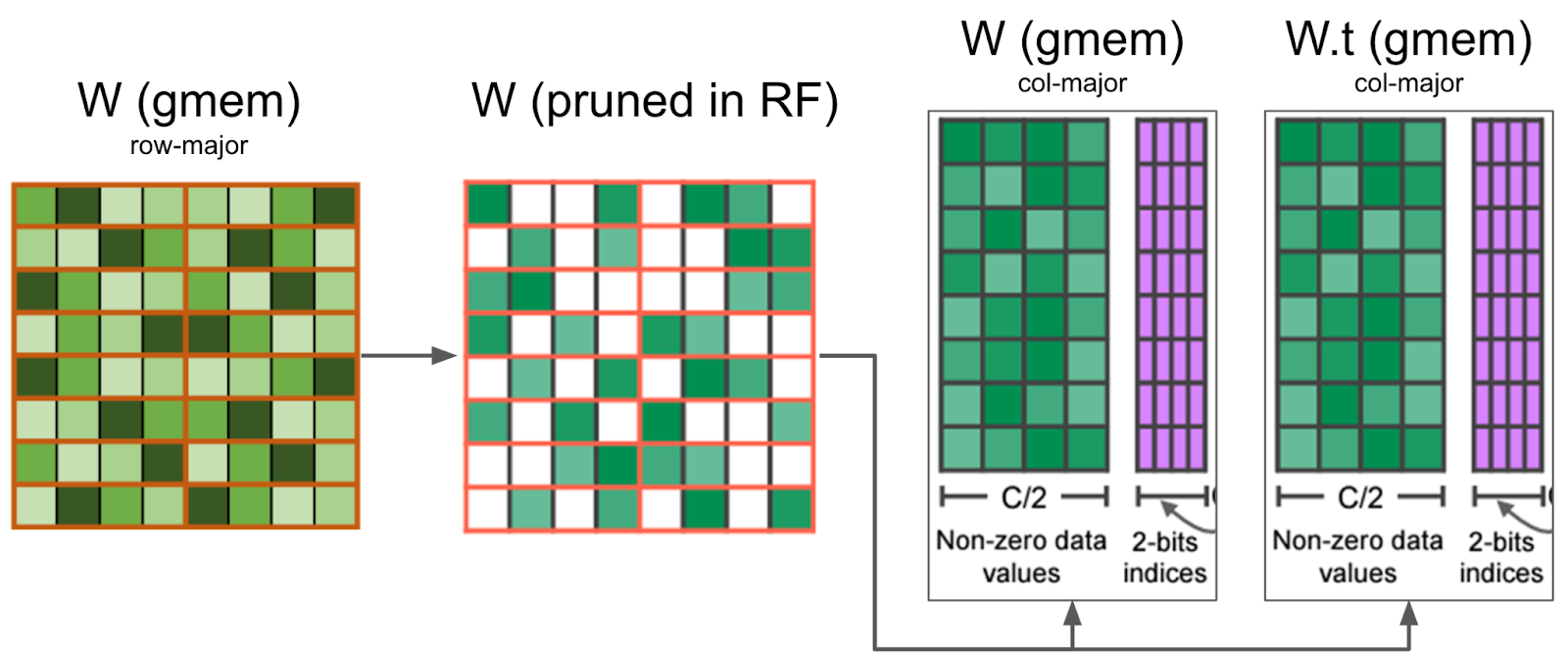
我们的内核在寄存器中剪枝权重矩阵,并将压缩后的值写入全局内存。它还同时剪枝 W.t,这是反向传播所需的,从而最小化内存 I/O。
处理反向传播时需要一些额外的转置技巧——底层硬件只支持第一个矩阵为稀疏的操作。在推理过程中进行权重稀疏化时,当我们需要计算 xW T 时,我们依靠转置属性来交换操作数的顺序。
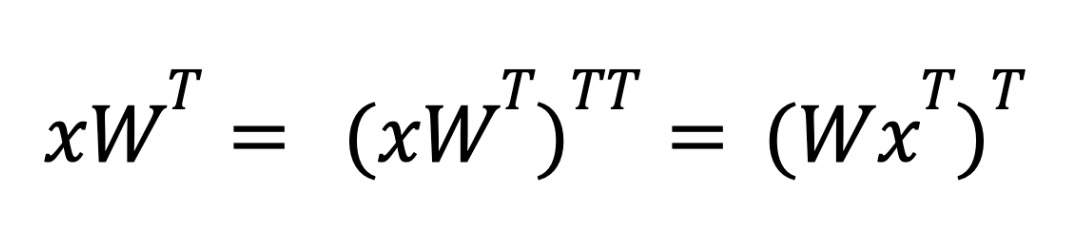
在推理过程中,我们使用 torch.compile 将外转置融合到后续的点操作中,以避免支付性能惩罚。
然而,在训练的反向传播过程中,我们没有后续的点操作可以融合。相反,我们利用 cuSPARSELt 指定结果矩阵的行/列布局的能力,将转置融合到矩阵乘法中。
2) 核心分块以提高内存-IO 效率
为了使我们的内核尽可能高效,我们希望合并我们的读写操作,因为我们发现内存 I/O 是主要的瓶颈。这意味着在 CUDA 线程中,我们希望每次读取/写入 128 字节的块,以便多个并行读取/写入可以由 GPU 内存控制器合并成一个请求。
因此,我们决定每个线程处理 4 个 4x4 的瓦片(即一个 8x8 的瓦片),而不是一个单独的 4x4 瓦片,因为 4x4x2=32 字节,这样我们可以操作 8x8x2=128 字节的块。
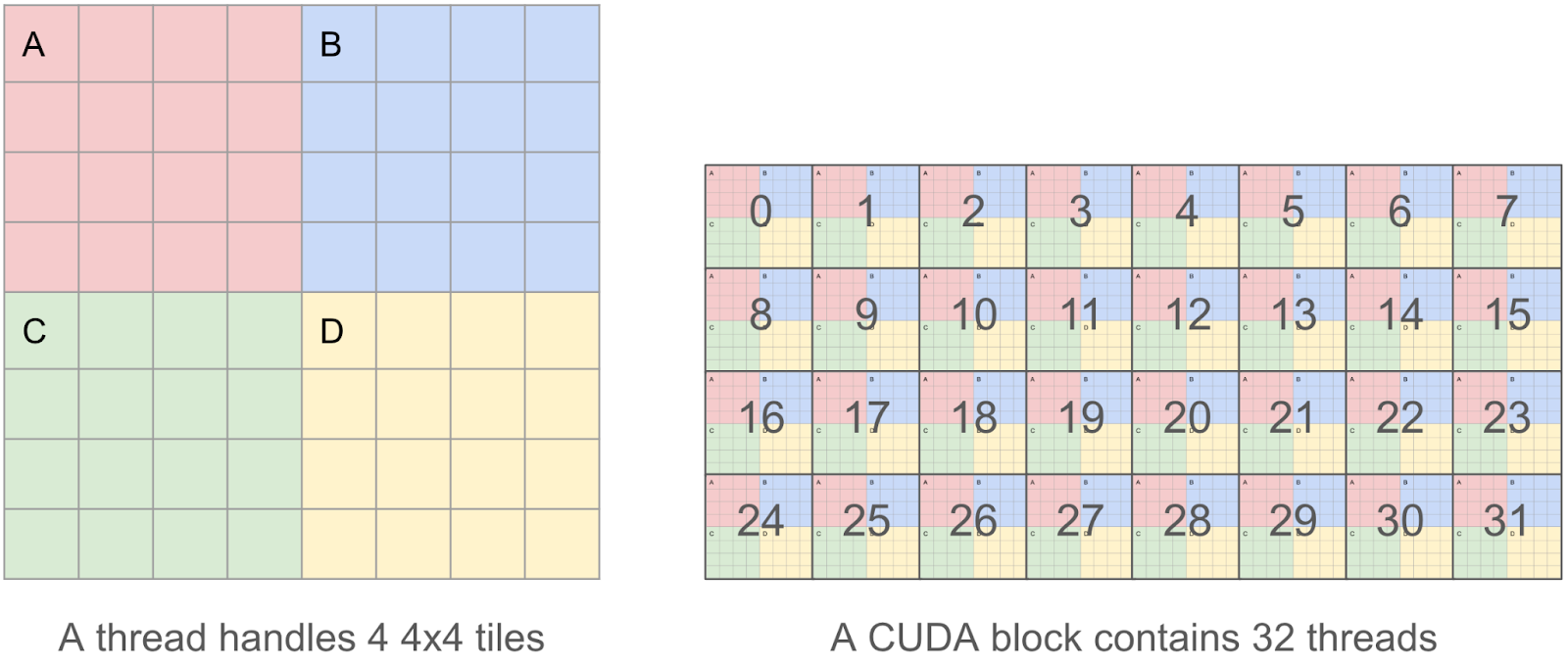
3) 在 4x4 瓦片内无 warp 发散地排序元素
对于线程内的每个单独的 4x4 瓦片,我们计算一个掩码,指定要剪枝的元素和要保留的元素。为此,我们排序所有 16 个元素,并贪婪地保留元素,只要它们不破坏我们的 2:4 行/列约束。这仅保留具有最大值的权重。
关键在于我们始终只对固定数量的元素进行排序,因此通过使用无分支排序网络,我们可以避免 warp 漏洞。
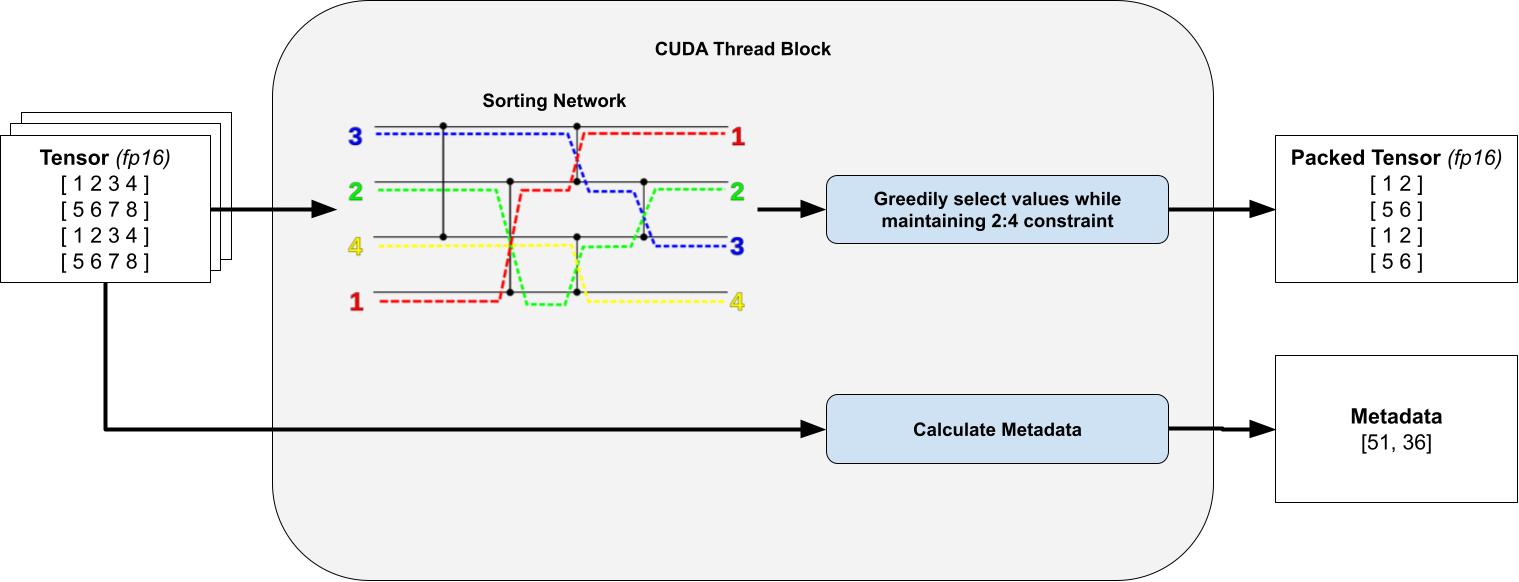
为了清晰起见,省略了转置打包张量和元数据。排序网络图来自维基百科。
当我们在线程块内部进行条件执行时,会发生 warp 漏洞。在 CUDA 中,同一工作组(线程块)中的工作项在硬件级别以批量的形式(warp)调度。如果我们有条件执行,使得同一批中的某些工作项运行不同的指令,那么当 warp 调度时,它们会被屏蔽,或者顺序调度。
例如,如果我们有一些代码如 if (condition) do(A) else do(B) ,其中条件由所有奇数编号的工作项满足,那么这个条件语句的总运行时间是 do(A) + do(B) ,因为我们将为所有奇数编号的工作项调度 do(A) ,屏蔽偶数编号的工作项,并为所有偶数编号的工作项调度 do(B) ,屏蔽奇数编号的工作项。此答案提供了更多关于 warp 漏洞的信息。
4) 编写压缩矩阵和元数据
一旦计算完成掩码,就必须将权重数据以压缩格式写回全局内存。这并不简单,因为数据需要保留在寄存器中,而且无法对寄存器进行索引(例如, C[i++] = a 阻止我们将 C 存储在寄存器中)。此外,我们发现 nvcc 使用的寄存器比预期多得多,这导致了寄存器溢出并影响了全局性能。我们将这个压缩矩阵以列主序格式写入全局内存,以提高写入效率。
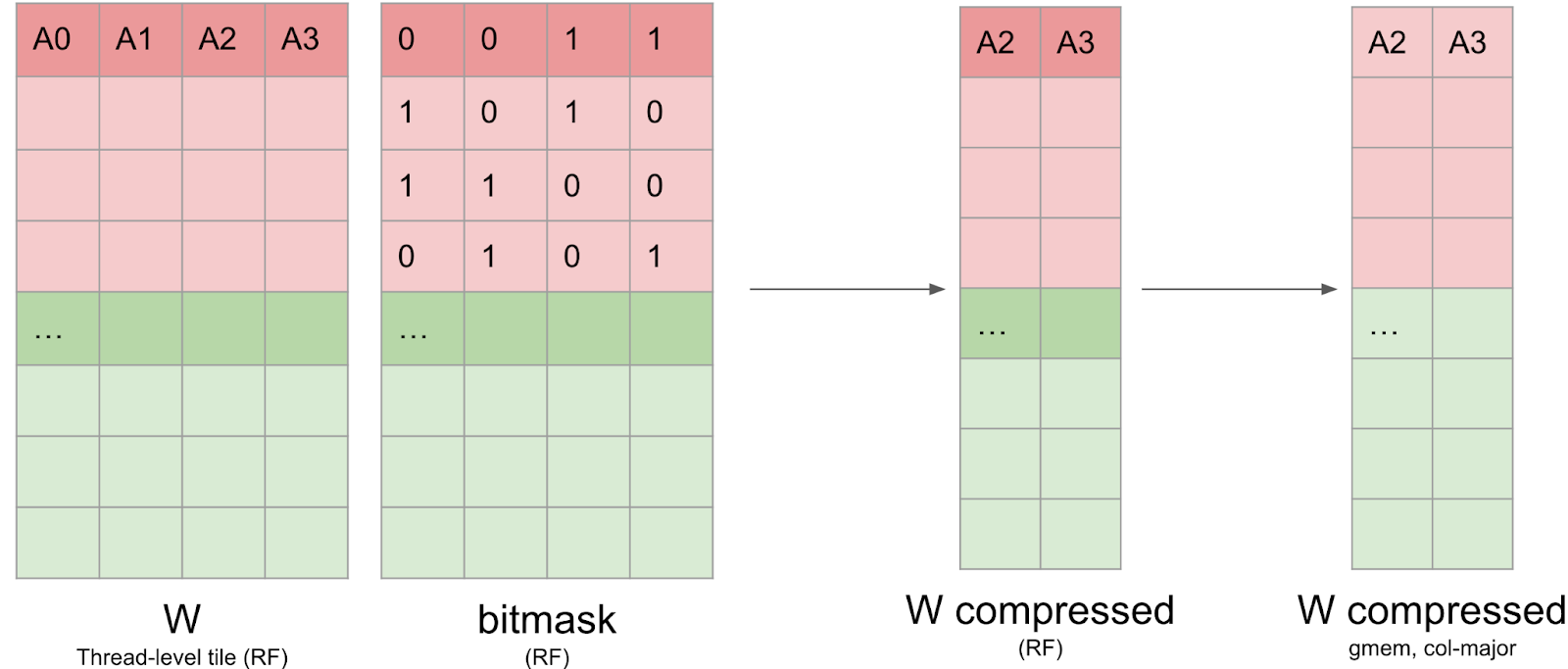
我们还需要编写 cuSPARSELt 元数据。这种元数据布局与开源 CUTLASS 库中的布局非常相似,并且针对通过 GEMM 内核的 PTX ldmatrix 指令高效加载到共享内存进行了优化。
然而,这种布局并不适合高效写入:元数据张量的前 128 位包含关于行 0、8、16 和 24 的前 32 列的元数据。回想一下,每个线程处理一个 8x8 的瓦片,这意味着这些信息分布在 16 个线程上。
我们依赖于一系列的扭曲-洗牌操作,分别对原始和转置表示进行一次,以写入元数据。幸运的是,这些数据仅占总 I/O 的不到 10%,因此我们可以承担不完全合并写入的成本。
DINOv2 稀疏训练:实验设置与结果
在我们的实验中,ViT-L 模型使用 DINOv2 方法在 ImageNet 上训练了 125k 步。所有实验均在 4x AMD EPYC 7742 64 核 CPU 和 4x NVIDIA A100-80GB GPU 上运行。在稀疏训练期间,模型在训练的前半部分启用 2:4 稀疏性,只有一半的权重被启用。这个权重稀疏掩码在每一步都会动态重新计算,因为权重在优化过程中会持续更新。在剩余的步骤中,模型以密集方式训练,最终产生一个没有 2:4 稀疏性的最终模型(除了 100%稀疏训练设置),然后对其进行评估。
| 训练设置 | ImageNet 1k 对数回归 |
| 0% 稀疏(125k 稠密步骤,基线) | 82.8 |
| 40% 稀疏(50k 稀疏 -> 75k 稠密步骤) | 82.9 |
| 60% 稀疏(75k 稀疏 -> 50k 稠密步骤) | 82.8 |
| 70% 稀疏(87.5k 稀疏 -> 37.5k 稠密步数) | 82.7 |
| 80% 稀疏(100k 稀疏 -> 25k 稠密步数) | 82.7 |
| 90% 稀疏(112.5k 稀疏 -> 12.5k 稠密步数) | 82.0 |
| 100% 稀疏(125k 稀疏步数) | 82.3 (2:4-稀疏模型) |
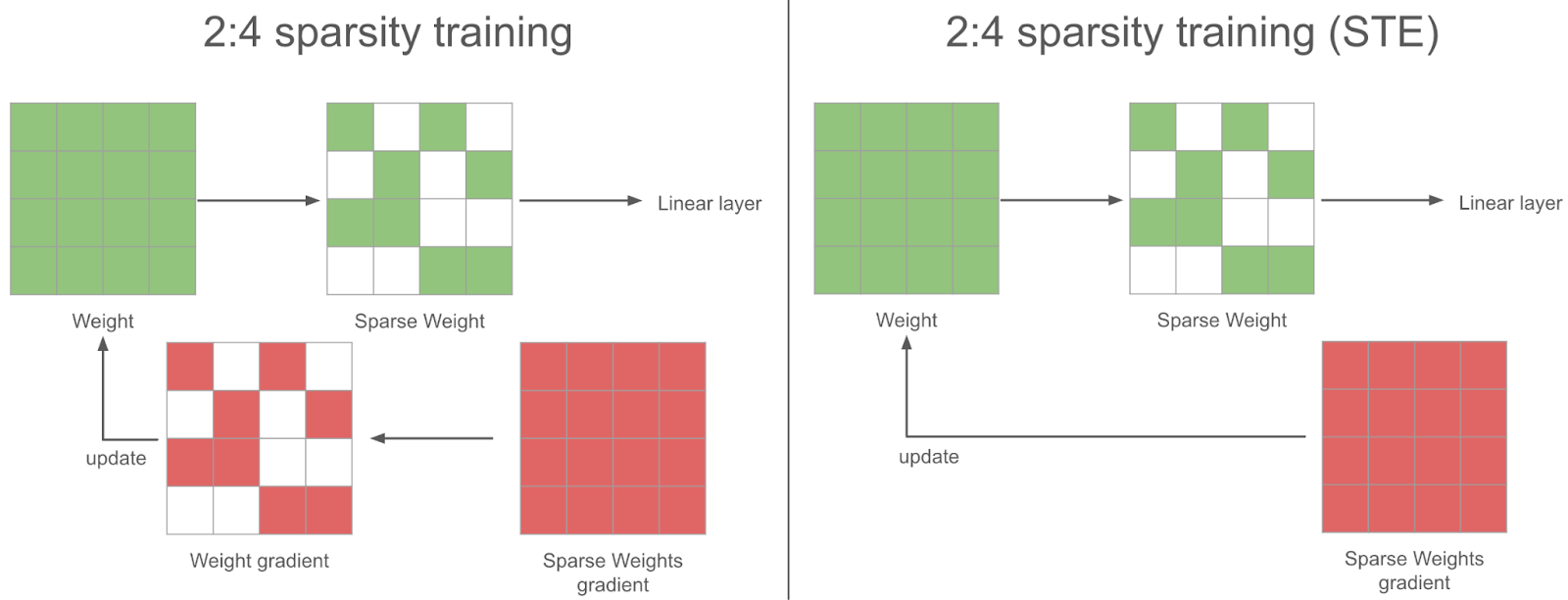
在稀疏训练步骤中,在反向传播过程中,我们获得了稀疏权重的密集梯度。为了梯度下降是有效的,我们应在将其用于优化器更新权重之前对梯度进行稀疏化。然而,我们没有这样做,而是使用完整的密集梯度来更新权重——我们发现这在实践中效果更好:这就是 STE(直接估计器)策略。换句话说,我们在每一步更新所有参数,即使是我们不使用的参数。
结论与未来工作
在这篇博客文章中,我们展示了如何使用半结构化稀疏性加速神经网络训练,并解释了我们面临的一些挑战。我们能够在 DINOv2 训练中实现 6%的端到端速度提升,同时精度仅下降了 0.1 pp。
该工作的扩展领域有几个:
- 扩展到新的稀疏模式:研究人员创建了新的稀疏模式,如 V:N:M 稀疏模式,它使用底层半结构化稀疏核以实现更大的灵活性。这对于将稀疏性应用于LLMs特别有趣,因为 2:4 稀疏性会降低精度太多,但我们已经看到了更通用的 N:M 模式的一些积极结果。
- 稀疏微调的性能优化:本文涵盖了从头开始的稀疏训练,但很多时候我们想要微调一个基础模型。在这种情况下,静态掩码可能足以保留精度,这将使我们能够进行额外的性能优化。
- 关于剪枝策略的更多实验:我们在网络的每个步骤计算掩码,但每 n 步计算一次掩码可能会产生更好的训练精度。总的来说,确定在训练期间使用半结构化稀疏性的最佳策略是一个开放的研究领域。
- 与 fp8 的兼容性:硬件也支持 fp8 半结构化稀疏性,原则上这种方法应该与 fp8 类似。实际上,我们需要编写类似的稀疏化内核,并且可能将它们与张量的缩放融合。
- 激活稀疏性:高效的稀疏化内核还可以在训练过程中对激活进行稀疏化。由于稀疏化开销与稀疏化矩阵大小线性增长,与权重张量相比,具有较大激活张量的设置可以从激活稀疏性中受益更多。此外,由于使用了 ReLU 或 GELU 激活函数,激活本身是稀疏的,这可以减少精度下降。
如果您对这些问题感兴趣,请随时在 torchao 上打开一个 issue / PR,torchao 是我们正在构建的用于架构优化技术(如量化和稀疏性)的社区。另外,如果您对稀疏性有一般兴趣,请在 CUDA-MODE (#sparsity)中与我们联系。